Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-30T21:43:42.706Z Has data issue: false hasContentIssue false
  • English
  • Français

Ramsey sets, the Ramsey ideal, and other classes over R

Published online by Cambridge University Press:  12 March 2014

Paul Corazza
Paul Corazza*
Affiliation:
Department of Mathematics, Maharishi International University, Faculty Mail Box 1088, Fairfield, IA 52556, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We improve results of Marczewski, Frankiewicz, Brown, and others comparing the ω-ideals of measure zero, meager, Marczewski measure zero, and completely Ramsey null sets; in particular, we remove CH from the hypothesis of many of Brown's constructions of sets lying in some of these ideals but not in others. We improve upon work of Marczewski by constructing, without CH, a nonmeasurable Marczewski measure zero set lacking the property of Baire. We extend our analysis of ω-ideals to include the completely Ramsey null sets relative to a Ramsey ultrafilter and obtain all 32 possible examples of sets in some ideals and not others, some under the assumption of MA, but most in ZFC alone. We also improve upon the known constructions of a Marczewski measure zero set which is not Ramsey by using a set theoretic hypothesis which is weaker than those used by other authors. We give several consistency proofs: one concerning the relative sizes of the covering numbers for the meager sets and the completely Ramsey null sets; another concerning the size of non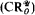; and a third concerning the size of add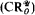. We also study those classes of perfect sets which are bases for the class of always first category sets.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 57 , Issue 4 , December 1992 , pp. 1441 - 1468
Copyright
Copyright © Association for Symbolic Logic 1992

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[AFP[Aniszczyk, , Frankiewicz, , and Plewik, , Remarks on (s) and Ramsey-measurable functions, Bulletin of the Polish Academy of Sciences. Mathematics, vol. 35 (1987), pp. 479–485.Google Scholar
[B[Brown, J., The Ramsey sets and related ω-algebras and ideals, Transactions of the American Mathematical Society (to appear).Google Scholar
[Ba[Baumgartner, J., Iterated forcing, Surveys in set theory (Mathias, A.R.D., editor), Cambridge University Press, London and New York, 1983, pp. 1–59.Google Scholar
[BC[Brown, J. and Cox, G., Classical theory of totally imperfect spaces, Real Analysis Exchange, vol. 7 (1982), pp. 1–39.Google Scholar
[BL[Baumgartner, J. and Laver, R., Iterated perfect set forcing, Annals of Mathematical Logic, vol. 17 (1979), pp. 271–288.CrossRefGoogle Scholar
[BP[Brown, J. and Prikry, K., Variations on Lusin's theorem, Transactions of the American Mathematical Society, vol. 302 (1987), pp. 77–85.Google Scholar
[C1[Corazza, P., Ramsey sets, the Ramsey ideal, and other classes over ℝ, Abstracts of the American Mathematical Society, vol. 9, no. 5 (1988), p. 348.Google Scholar
[C2[Corazza, P., The generalized Borel conjecture and strongly proper orders, Transactions of the American Mathematical Society, vol. 316 (1989), pp. 115–140.CrossRefGoogle Scholar
[E[Ellentuck, E., A new proof that analytic sets are Ramsey, this Journal, vol. 39 (1974), pp. 163–165.Google Scholar
[F1[Fremlin, D. H., Cichon's diagram, presented at the Seminaire Initiation a l'Analyse, G. Choquet, M. Rogalski, J. Saint Raymond, at the Universite Pierre et Marie Curie, Paris, 23e annee, 1983/1984, #5, 13 pp.Google Scholar
[F2[Fremlin, D. H., Consequences of Martin's Axiom, Cambridge University Press, London and New York, 1984.CrossRefGoogle Scholar
[G[Grzegorek, E., Always of the first category sets, Proceedings of the 12th Winter School on Abstract Analysis, Srni (Bohemian Weald), 01 15–28, 1984, Section of Topology, Supplemento ai Rendiconti del Circolo Matematico di Palermo, Serie II, vol. 6 (1984), pp. 139–147.Google Scholar
[GP[Galvin, F. and Prikry, K., Borel sets and Ramsey's theorem, this Journal, vol. 38 (1973), pp. 193–198.Google Scholar
[J[Jech, T., Set theory, Academic Press, San Diego, CA, 1978.Google Scholar
[JMS[Judah, H., Miller, A. W., and Shelah, S., Sacks forcing, haver forcing, and Martin's Axiom, Arch. Math. Logic, vol. 31 (1992), pp. 145–161.CrossRefGoogle Scholar
[L[Laver, R., On the consistency of Borel's conjecture, Acta Mathematica, vol. 137 (1976), pp. 151–169.CrossRefGoogle Scholar
[Lo[Louveau, A., Une méthode topologigue pour I 'etude de la propriété de Ramsey, Israel Journal of Mathematics, vol. 23 (1976), pp. 97–116.CrossRefGoogle Scholar
[K1[Kunen, K., Set theory, an introduction to independence proofs, North-Holland, Amsterdam, 1980.Google Scholar
[K2[Kunen, K., Some points in βN, Mathematical Proceedings of the Cambridge Philosophical Society, vol. 80 (1976), pp. 385–398.CrossRefGoogle Scholar
[M[Moschovakis, Y., Descriptive set theory, North-Holland, Amsterdam, 1980.Google Scholar
[Ma1[Szpilrajn, E. (Marczewski), On absolutely measurable sets and functions, Compte Rendu de la Soc. Sci. Varsovie (3), vol. 30 (1937), pp. 39–68. (Polish)Google Scholar
[Ma2[Szpilrajn, E. (Marczewski), Sur une classe de fonctions de W. Sierpinski et la classe correspondante d'ensembles, Fundamenta Mathematicae, vol. 24 (1935), pp. 17–34.CrossRefGoogle Scholar
[Mi1[Miller, A. W., Some properties of measure and category, Transactions of the American Mathematical Society, vol. 266 (1981), pp. 93–114.CrossRefGoogle Scholar
[Mi2[Szpilrajn, E. (Marczewski), Special subsets of the real line, Handbook of set-theoretic topology (Kunen, K. and Vaughan, J., editors), North-Holland, Amsterdam, 1984.Google Scholar
[Mi3[Szpilrajn, E. (Marczewski), Private communication, 08, 1991.Google Scholar
[Mo[Morgan, J., Category bases, Marcel Dekker, New York, 1990.Google Scholar
[Ms[Mathias, A., Happy families, Annals of Mathematical Logic, vol. 12 (1977), pp. 59–111.CrossRefGoogle Scholar
[O[Oxtoby, J., Measure and category, a survey of the analogies between topological and measure spaces, Springer-Verlag, Berlin and New York, 1980.Google Scholar
[R[Royden, H. L., Real analysis, MacMillan, New York, 1968.Google Scholar
[S[Sierpinski, W., Sur les ensembles jouissant de la proprieté de Baire, Fundamenta Mathematicae, vol. 23 (1934), pp. 121–124.CrossRefGoogle Scholar
[Si[Silver, J., Every analytic set is Ramsey, this Journal, vol. 35 (1970), pp. 60–64.Google Scholar
[So[Solomon, R., Families of sets and functions, Czechoslovak Mathematical Journal, vol. 27 (1977), pp. 556–559.CrossRefGoogle Scholar
[W1[Walsh, J. T., Marczewski sets, measure and the Baire property, PhD Dissertation, Auburn University, 1984.CrossRefGoogle Scholar
[W2[Walsh, J. T., Marczewski sets, measure and the Baire property II, Proceedings of the American Mathematical Society, vol 106 (1989), pp. 1027–1030.Google Scholar