Hostname: page-component-6bf8c574d5-vmclg Total loading time: 0 Render date: 2025-02-17T13:50:05.620Z Has data issue: false hasContentIssue false
  • English
  • Français

PUNCTUAL CATEGORICITY AND UNIVERSALITY

Part of: Computability and recursion theory

Published online by Cambridge University Press:  22 October 2020

ROD DOWNEY ,
NOAM GREENBERG ,
ALEXANDER MELNIKOV ,
KENG MENG NG  and
DANIEL TURETSKY
ROD DOWNEY
Affiliation:
SCHOOL OF MATHEMATICS AND STATISTICS VICTORIA UNIVERSITY OF WELLINGTONWELLINGTON, PO BOX 600, NEW ZEALANDE-mail: [email protected]: [email protected]
NOAM GREENBERG
Affiliation:
SCHOOL OF MATHEMATICS AND STATISTICS VICTORIA UNIVERSITY OF WELLINGTONWELLINGTON, PO BOX 600, NEW ZEALANDE-mail: [email protected]: [email protected]
ALEXANDER MELNIKOV
Affiliation:
MASSEY UNIVERSITY AUCKLAND PRIVATE BAG 102904, NORTH SHOREAUCKLAND0745, NEW ZEALANDE-mail: [email protected]
KENG MENG NG
Affiliation:
SCHOOL OF PHYSICAL AND MATHEMATICAL SCIENCES DIVISION OF MATHEMATICAL SCIENCES NANYANG TECHNOLOGICAL UNIVERSITY, SINGAPOREE-mail: [email protected]
DANIEL TURETSKY
Affiliation:
SCHOOL OF MATHEMATICS AND STATISTICS VICTORIA UNIVERSITY OF WELLINGTONWELLINGTON, PO BOX 600, NEW ZEALANDE-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We describe punctual categoricity in several natural classes, including binary relational structures and mono-unary functional structures. We prove that every punctually categorical structure in a finite unary language is 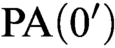${\text {PA}}(0')$-categorical, and we show that this upper bound is tight. We also construct an example of a punctually categorical structure whose degree of categoricity is 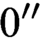$0''$. We also prove that, with a bit of work, the latter result can be pushed beyond 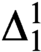$\Delta ^1_1$, thus showing that punctually categorical structures can possess arbitrarily complex automorphism orbits.

As a consequence, it follows that binary relational structures and unary structures are not universal with respect to primitive recursive interpretations; equivalently, in these classes every rich enough interpretation technique must necessarily involve unbounded existential quantification or infinite disjunction. In contrast, it is well-known that both classes are universal for Turing computability.

Keywords

primitive recursioncomputable structurespunctual computability

MSC classification

Primary: 03D45: Theory of numerations, effectively presented structures
Secondary: 03D20: Recursive functions and relations, subrecursive hierarchies 03D99: None of the above, but in this section
Type
Articles
Information
The Journal of Symbolic Logic , Volume 85 , Issue 4 , December 2020 , pp. 1427 - 1466
Check for updates
Copyright
© The Association for Symbolic Logic 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Ash, C. and Knight, J., Computable Structures and the Hyperarithmetical Hierarchy, Studies in Logic and the Foundations of Mathematics, vol. 144, North-Holland, Amsterdam, 2000.Google Scholar
Bazhenov, N., Downey, R., Kalimullin, I., and Melnikov, A., Foundations of online structure theory. Bulletin of Symbolic Logic, vol. 25 (2019), no. 2, pp. 141–181.CrossRefGoogle Scholar
Bazhenov, N., Harrison-Trainor, M., Kalimullin, I., Melnikov, A., and Ng, K. M., Automatic and polynomial-time algebraic structures. this Journal, vol. 04 (2019), pp. 1–32.Google Scholar
Bazhenov, N. A., Frolov, A. N., Kalimullin, I. S., and Melnikov, A. G. E., Computability of distributive lattices. Sibirskii Matematicheskii Zhurnal, vol. 58 (2017), no. 6, pp. 1236–1251.Google Scholar
Cenzer, D. A. and Remmel, J. B., Polynomial-time Abelian groups. Annals of Pure and Applied Logic, vol. 56 (1992), no. 1-3, pp. 313–363.CrossRefGoogle Scholar
Cenzer, D., Downey, R. G., Remmel, J. B., and Uddin, Z., Space complexity of abelian groups. Archive for Mathematical Logic, vol. 48 (2009), no. 1, pp. 115–140.CrossRefGoogle Scholar
Cenzer, D. and Remmel, J. B., Complexity theoretic model theory and algebra, Handbook of Recursive Mathematics, vol. 1 (Ershov, Y. L., Goncharov, S. S., Nerode, A., and Remmel, J. B., editors), Studies in Logic and the Foundations of Mathematics, vol. 138, North-Holland, Amsterdam, 1998, pp. 381–513.CrossRefGoogle Scholar
Downey, R. G., Kach, A. M., Lempp, S., Lewis-Pye, A. E. M., Montalbán, A., and Turetsky, D. D., The complexity of computable categoricity. Advances in Mathematics, vol. 268 (2015), pp. 423–466.CrossRefGoogle Scholar
Downey, R., Harrison-Trainor, M., Kalimullin, I., Melnikov, A., and Turetsky, D., Graphs are not universal for online computability, Journal of Computer and System Sciences, Vol. 112, September (2020), pp 1–12.CrossRefGoogle Scholar
Downey, R., Hirschfeldt, D., and Khoussainov, B., Uniformity in the theory of computable structures. Algebra Logika, vol. 42 (2003), no. 5, pp. 566–593, 637.CrossRefGoogle Scholar
Downey, R., Melnikov, A., and Ng, K. M.. Foundations of online structure theory II: The operator approach, preprint, 2020.Google Scholar
Ershov, Y. and Goncharov, S., Constructive Models. Siberian School of Algebra and Logic, Consultants Bureau, New York, 2000.CrossRefGoogle Scholar
Goncharov, S., The problem of the number of nonautoequivalent constructivizations. Algebra i Logika, vol. 19 (1980), no. 6, 621–639, 745.Google Scholar
Goncharov, S., Groups with a finite number of constructivizations. Doklady Akademii Nauk, vol. 256 (1981), no. 2, pp. 269–272.Google Scholar
Goncharov, S. S., Molokov, A. V., and Romanovskiĭ, N. S., Nilpotent groups of finite algorithmic dimension. Sibirskii Matematicheskii Zhurnal, vol. 30 (1989), no. 1, pp. 82–88.Google Scholar
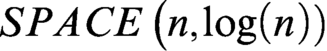Grigorieff, S., Every recursive linear ordering has a copy in $DTIME$- $SPACE\left(n,\mathit{\log}(n)\right)$. this Journal, vol. 55 (1990), no. 1, pp. 260–276.Google Scholar
Gromov, M., Metric Structures for Riemannian and Non-Riemannian Spaces. Modern Birkhäuser Classics, Birkhäuser, Boston, 2007.Google Scholar
Harrison-Trainor, M., Melnikov, A., Miller, R., and Montalbán, A., Computable functors and effective interpretability, this Journal, vol. 82 (2017), no. 1, pp. 77–97.Google Scholar
Hirschfeldt, D. R., Some questions in computable mathematics, Computability and Complexity, Lecture Notes in Computer Science, vol. 10010, Springer, Cham, 2017, pp. 22–55.CrossRefGoogle Scholar
Hirschfeldt, D., Khoussainov, B., Shore, R., and Slinko, A., Degree spectra and computable dimensions in algebraic structures. Annals of Pure and Applied Logic, vol. 115 (2002), no. 1–3, pp. 71–113.CrossRefGoogle Scholar
Kalimullin, I., Melnikov, A., and Montalbán, A., Definability and punctual computability, preprint, 2019.Google Scholar
Kalimullin, I., Melnikov, A., and Ng, K. M., Algebraic structures computable without delay. Theoretical Computer Science, vol. 674 (2017), pp. 73–98.CrossRefGoogle Scholar
Kalimullin, I. and Miller, R., Primitive recursive fields and categoricity. Algebra and Logic, vol. 58 (2019), no. 1, pp. 132–138.Google Scholar
Khoussainov, B. and Nerode, A., Open questions in the theory of automatic structures. Bulletin of the European Association for Theoretical Computer Science, vol. 94 (2008), pp. 181–204.Google Scholar
Kierstead, H. A., Recursive and on-line graph coloring, Handbook of Recursive Mathematics, vol. 2 (Ershov, Y. L., Goncharov, S. S., Nerode, A., and Remmel, J. B., editors), Studies in Logic and the Foundations of Mathematics, vol. 139, North-Holland, Amsterdam, 1998, pp. 1233–1269.Google Scholar
Kierstead, H. A., Penrice, S. G., and Trotter, W. T. Jr., On-line coloring and recursive graph theory. SIAM Journal on Discrete Mathematics, vol. 7 (1994), pp. 72–89.CrossRefGoogle Scholar
Melnikov, A. G., Eliminating unbounded search in computable algebra, Unveiling Dynamics and Complexity, Lecture Notes in Computer Science, vol. 10307, Springer, Cham, 2017, pp.77–87.CrossRefGoogle Scholar
Melnikov, A. G. and Nies, A., The classification problem for compact computable metric spaces, The Nature of Computation. Logic, Algorithms, Applications (Bonizzoni, P., Brattka, V., and Löwe, B., editors), Springer, Berlin, Heidelberg, 2013, pp. 320–328.CrossRefGoogle Scholar
Miller, R., Poonen, B., Schoutens, H., and Shlapentokh, A., A computable functor from graphs to fields, this Journal, vol. 83 (2018), no. 1, pp. 326–348.Google Scholar