Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Jäger, Gerhard
1980.
Zur Beweistheorie Der Kripke-Platek-Mengenlehre Über Den Natürlichen Zahlen.
Archiv für Mathematische Logik und Grundlagenforschung,
Vol. 22,
Issue. 3-4,
p.
121.
Schütte, Kurt
1980.
Beweistheoretische Abgrenzung von Teilsystemen der Analysis.
Monatshefte für Mathematik,
Vol. 90,
Issue. 1,
p.
1.
Pohlers, W.
1981.
Cut-elimination for impredicative infinitary systems part I. Ordinal-analysis for ID1.
Archiv für Mathematische Logik und Grundlagenforschung,
Vol. 21,
Issue. 1,
p.
113.
Pohlers, W.
1982.
Logic, Methodology and Philosophy of Science VI, Proceedings of the Sixth International Congress of Logic, Methodology and Philosophy of Science.
Vol. 104,
Issue. ,
p.
123.
Jäger, Gerhard
1982.
Proceedings of the Herbrand Symposium.
Vol. 107,
Issue. ,
p.
137.
Goondeev, Lev
1982.
The L. E. J. Brouwer Centenary Symposium, Proceedings of the Conference held in Noordwijkerhout.
Vol. 110,
Issue. ,
p.
123.
Jäger, Gerhard
1983.
A well-ordering proof for Feferman's theoryT 0.
Archiv für Mathematische Logik und Grundlagenforschung,
Vol. 23,
Issue. 1,
p.
65.
Buchholz, W.
1986.
A new system of proof-theoretic ordinal functions.
Annals of Pure and Applied Logic,
Vol. 32,
Issue. ,
p.
195.
Crossley, John N.
and
Kister, Jane Bridge
1987.
Natural well-orderings.
Archiv für Mathematische Logik und Grundlagenforschung,
Vol. 26,
Issue. 1,
p.
57.
Rathjen, Michael
1994.
Collapsing functions based on recursively large ordinals: A well-ordering proof for KPM.
Archive for Mathematical Logic,
Vol. 33,
Issue. 1,
p.
35.
Pohlers, Wolfram
1998.
Handbook of Proof Theory.
Vol. 137,
Issue. ,
p.
209.
Rathjen, Michael
2005.
Replacement versus collection and related topics in constructive Zermelo–Fraenkel set theory.
Annals of Pure and Applied Logic,
Vol. 136,
Issue. 1-2,
p.
156.
Leigh, G.E.
2013.
A proof-theoretic account of classical principles of truth.
Annals of Pure and Applied Logic,
Vol. 164,
Issue. 10,
p.
1009.
Fujimoto, Kentaro
2015.
Notes on some second-order systems of iterated inductive definitions and Π11-comprehensions and relevant subsystems of set theory.
Annals of Pure and Applied Logic,
Vol. 166,
Issue. 4,
p.
409.
Pohlers, Wolfram
2017.
Feferman on Foundations.
Vol. 13,
Issue. ,
p.
209.
Arai, Toshiyasu
2020.
Ordinal Analysis with an Introduction to Proof Theory.
p.
97.
Diana Schmidt
2020.
Well-Quasi Orders in Computation, Logic, Language and Reasoning.
Vol. 53,
Issue. ,
p.
351.
Jäger, Gerhard
2022.
Axiomatic Thinking II.
p.
9.
Jäger, Gerhard
and
Rathjen, Michael
2024.
Admissible extensions of subtheories of second order arithmetic.
Annals of Pure and Applied Logic,
Vol. 175,
Issue. 7,
p.
103425.
Jäger, Gerhard
2024.
Tame and full strict-Π11 reflection: A proof-theoretic approach.
Journal of Logic and Computation,
Vol. 34,
Issue. 6,
p.
1082.
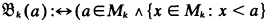 is wellordered) with Mκ ≔ {x ∈
is wellordered) with Mκ ≔ {x ∈ 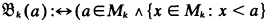 and 0 ≤ κ ≤ N. Obviously the predicates
and 0 ≤ κ ≤ N. Obviously the predicates 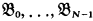 are definable in IDNi with the defining axioms:
are definable in IDNi with the defining axioms: