Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Clote, P.
1990.
Bounded arithmetic and computational complexity.
p.
186.
Clote, P.
1990.
ALOGTIME and a conjecture of S.A. Cook.
p.
181.
Buss, Samuel R.
1991.
Propositional consistency proofs.
Annals of Pure and Applied Logic,
Vol. 52,
Issue. 1-2,
p.
3.
Urquhart, Alasdair
1992.
Logic from Computer Science.
Vol. 21,
Issue. ,
p.
597.
Clote, Peter
1992.
ALOGTIME and a conjecture of S.A. Cook.
Annals of Mathematics and Artificial Intelligence,
Vol. 6,
Issue. 1-3,
p.
57.
Pitassi, T.
and
Urquhart, A.
1992.
The complexity of the Hajos calculus.
p.
187.
Cook, Stephen
and
Urquhart, Alasdair
1993.
Functional interpretations of feasibly constructive arithmetic.
Annals of Pure and Applied Logic,
Vol. 63,
Issue. 2,
p.
103.
Adamowicz, Zofia
1994.
First European Congress of Mathematics Paris, July 6–10, 1992.
p.
299.
Adamowicz, Zofia
1994.
First European Congress of Mathematics.
p.
299.
Pitassi, Toniann
and
Urquhart, Alasdair
1995.
The Complexity of the Hajós Calculus.
SIAM Journal on Discrete Mathematics,
Vol. 8,
Issue. 3,
p.
464.
Pudlák, Pavel
and
Buss, Samuel R.
1995.
Computer Science Logic.
Vol. 933,
Issue. ,
p.
151.
Takeuti, Gaisi
1995.
Logic and Computational Complexity.
Vol. 960,
Issue. ,
p.
221.
Krajíček, Jan
1995.
Feasible Mathematics II.
p.
284.
Urquhart, Alasdair
1995.
The Complexity of Propositional
Proofs.
Bulletin of Symbolic Logic,
Vol. 1,
Issue. 4,
p.
425.
Buss, Samuel R.
1995.
Some remarks on lengths of propositional proofs.
Archive for Mathematical Logic,
Vol. 34,
Issue. 6,
p.
377.
Bonet, Maria Luisa
Buss, Samuel R.
and
Pitassi, Toniann
1995.
Feasible Mathematics II.
p.
30.
Pudlák, Pavel
1995.
Proceedings of the International Congress of Mathematicians.
p.
288.
Krajíček, Jan
and
Pudlák, Pavel
1995.
Logic and Computational Complexity.
Vol. 960,
Issue. ,
p.
210.
Pudlák, Pavel
1996.
Collegium Logicum.
Vol. 2,
Issue. ,
p.
65.
Pudlák, Pavel
1996.
Gödel ’96.
Vol. 6,
Issue. ,
p.
81.


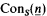 saying that there is no proof of contradiction in
saying that there is no proof of contradiction in 