Article contents
Propositional logic based on the dynamics of belief
Published online by Cambridge University Press: 12 March 2014
Extract
In this article propositions will be identified with a certain kind of changes of belief. The intended interpretation is that a proposition is characterised by the change it would induce if added to a state of belief. Propositions will thus be defined as functions from states of belief to states of belief. A set of postulates concerning the properties and existence of propositions will be formulated. A proposition will be said to be a tautology iff it is the identity function on states of belief. The main result is that the logic determined by the set of postulates is intuitionistic propositional logic.
The basic epistemic concept is that of a belief model, which is defined as a pair 〈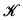 ,
, 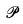 〉, where
〉, where 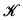 is a nonempty set and
is a nonempty set and 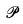 is a class of functions from
is a class of functions from 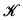 to
to 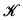 . The elements in
. The elements in 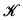 will be called states of belief and they will be denoted K, K′,…. A discussion of the epistemological interpretation of the states of belief can be found in Gärdenfors [2]. Here, no assumptions about the structure of the elements in
will be called states of belief and they will be denoted K, K′,…. A discussion of the epistemological interpretation of the states of belief can be found in Gärdenfors [2]. Here, no assumptions about the structure of the elements in 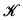 will be made.
will be made.
The elements in 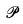 will be called propositions, and A, B, C, … will be used as variables over
will be called propositions, and A, B, C, … will be used as variables over 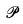 . Functions from states of belief to states of belief can be characterised as epistemic inputs. The intended interpretation of the functions in
. Functions from states of belief to states of belief can be characterised as epistemic inputs. The intended interpretation of the functions in 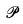 is that they correspond to changes of belief where the new evidence is accepted as “certain” or “known” in the resulting state of belief. This means that not all functions defined on
is that they correspond to changes of belief where the new evidence is accepted as “certain” or “known” in the resulting state of belief. This means that not all functions defined on 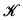 can properly be called propositions.
can properly be called propositions.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1985
References
REFERENCES
- 6
- Cited by


