Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-20T08:31:19.646Z Has data issue: false hasContentIssue false
  • English
  • Français

PROOF-THEORETIC STRENGTHS OF WEAK THEORIES FOR POSITIVE INDUCTIVE DEFINITIONS

Published online by Cambridge University Press:  23 October 2018

TOSHIYASU ARAI
TOSHIYASU ARAI*
Affiliation:
GRADUATE SCHOOL OF SCIENCE, CHIBA UNIVERSITY 1-33, YAYOI-CHO, INAGE-KU CHIBA, 263-8522, JAPANE-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this article the lightface 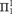${\rm{\Pi }}_1^1$-Comprehension axiom is shown to be proof-theoretically strong even over 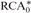${\rm{RCA}}_0^{\rm{*}}$, and we calibrate the proof-theoretic ordinals of weak fragments of the theory 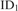${\rm{I}}{{\rm{D}}_1}$ of positive inductive definitions over natural numbers. Conjunctions of negative and positive formulas in the transfinite induction axiom of 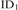${\rm{I}}{{\rm{D}}_1}$ are shown to be weak, and disjunctions are strong. Thus we draw a boundary line between predicatively reducible and impredicative fragments of 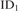${\rm{I}}{{\rm{D}}_1}$.

Keywords

03F35predicativityproof-theoretic ordinals
Type
Articles
Information
The Journal of Symbolic Logic , Volume 83 , Issue 3 , September 2018 , pp. 1091 - 1111
Copyright
Copyright © The Association for Symbolic Logic 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Afshari, B. and Rathjen, M., A note on the theory of positive induction, $ID_1^{\rm{*}}$.. Archive for Mathematical Logic, vol. 49 (2010), pp. 275–281.CrossRefGoogle Scholar
Buchholz, W., A new system of proof-theoretic ordinal functions. Annals of Pure and Applied Logic, vol. 32 (1986), pp. 195–208.CrossRefGoogle Scholar
Buchholz, W., A simplified version of local predicativity, Proof Theory (Aczel, P. H. G., Simmons, H., and Wainer, S. S., editors), Cambridge University Press, Cambridge, 1992, pp. 115–147.Google Scholar
Buchholz, W., A survey on ordinal notations around the Bachmann-Howard ordinal, Advances in Proof Theory (Kahle, R., Strahm, T., and Studer, T., editors), Birkhäuser, Basel, 2016, pp. 1–29.Google Scholar
Jäger, G. and Strahm, T., Some theories with positive induction of ordinal strength $\varphi \omega 0$., this JOURNAL, vol. 61 (1996), pp. 818–842.Google Scholar
Jäger, G. and Strahm, T., Bar induction and ω model reflection. Annals of Pure and Applied Logic, vol. 97 (1999), pp. 221–230.CrossRefGoogle Scholar
Probst, D., The proof-theoretic analysis of transfinitely iterated quasi least fixed points, this JOURNAL, vol. 71 (2006), pp. 721–746.Google Scholar
Rathjen, M. and Weiermann, A., Proof-theoretic investigations on Kruskal’s theorem. Annals of Pure and Applied Logic, vol. 60 (1993), pp. 49–88.CrossRefGoogle Scholar
Simpson, S., Subsystems of Second Order Arithmetic, second ed., Cambridge University Press, Cambridge, 2009.CrossRefGoogle Scholar
Van der Meeren, J., Connecting the Two Worlds: Well-partial-orders and Ordinal Notation Systems. Dissertation, Universiteit Gent, 2015.Google Scholar
Van der Meeren, J., Rathjen, M., and Weiermann, A., An order-theoretic characterization of the Howard-Bachmann-hierarchy. Archive for Mathematical Logic, vol. 56 (2017), pp. 79–118.CrossRefGoogle Scholar