Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Wilkie, Alex J.
2009.
2008 European Summer Meeting of the Association for Symbolic Logic. Logic Colloquium '08.
The Bulletin of Symbolic Logic,
Vol. 15,
Issue. 1,
p.
95.
Afshari, Bahareh
and
Rathjen, Michael
2010.
A note on the theory of positive induction, $${{\rm ID}^*_1}$$.
Archive for Mathematical Logic,
Vol. 49,
Issue. 2,
p.
275.
Leigh, Graham Emil
and
Rathjen, Michael
2010.
An ordinal analysis for theories of self-referential truth.
Archive for Mathematical Logic,
Vol. 49,
Issue. 2,
p.
213.
Ranzi, Florian
and
Strahm, Thomas
2014.
A note on the theory SID<ω of stratified induction.
Mathematical Logic Quarterly,
Vol. 60,
Issue. 6,
p.
487.
Jäger, Gerhard
and
Probst, Dieter
2015.
Gentzen's Centenary.
p.
425.
Ranzi, Florian
and
Strahm, Thomas
2019.
A flexible type system for the small Veblen ordinal.
Archive for Mathematical Logic,
Vol. 58,
Issue. 5-6,
p.
711.
Sato, Kentaro
2024.
A new model construction by making a detour via intuitionistic theories IV: A closer connection between KPω and BI.
Annals of Pure and Applied Logic,
Vol. 175,
Issue. 7,
p.
103422.


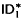 . This theory is obtained from the well-known theory ID
. This theory is obtained from the well-known theory ID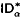 . Thus, we eventually know that
. Thus, we eventually know that