Article contents
Proof of a conjecture of Goodman
Published online by Cambridge University Press: 12 March 2014
Extract
In Chapter X of The Structure of appearance the concept of linear array is given in terms of a two-place predicate “M” for matching. Also given in terms of “M” is the two-place predicate “B” for besideness. It is unnecessary to discuss here the formal definitions, since Goodman has proved that they are adequate to describe our presystematic ideas of linear array and besideness. Thus, we shall be concerned with a finite collection of elements with an assigned order satisfying:
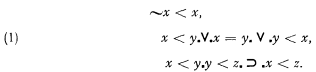
This order is not uniquely defined by the relation M; either of the two end points may be taken as the ‘first.’ We shall represent the order in diagrams by the convention that x is to the left of y if x < y. For x ≠ y, we shall define S(x, y), the distance between x and y, as one more than the number of elements strictly between them, in the order <; also, S(x, x) = 0. Thus S(x, y) = 1 if and only if x is beside y. The order is connected with the reflexive and symmetric matching relation M by the conditions
(2) Bx, y ⊃ Mx, y,
(3) Mx, y▪x ≤; u ≤ ν ≤ y▪ ⊃ ▪Mu, ν.
Condition (3) is what Goodman calls the weak mapping rule. All arrays considered here must satisfy (3). To avoid trivial cases, we shall assume that not all elements match. There is a strong mapping rule,
(4) Mx, y▪ ∼Mu, ν▪ ▪ ▪S(x, y) < S(u, ν),
which it is desirable, but not necessary, for arrays to satisfy. An array which does satisfy (4) is called regular.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1954
References
1 Nelson Goodman, Harvard University Press, 1951.
2 Ibid., Chapter X, § 6.
- 2
- Cited by


