Article contents
Prime numbers and factorization in IE1 and weaker systems
Published online by Cambridge University Press: 12 March 2014
Abstract
We show that IE1 proves that every element greater than 1 has a unique factorization into prime powers, although we have no way of recovering the exponents from the prime powers which appear. The situation is radically different in Bézout models of open induction. To facilitate the construction of counterexamples, we describe a method of changing irreducibles into powers of irreducibles, and we define the notion of a frugal homomorphism into 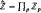 , the product of the p-adic integers for each prime p.
, the product of the p-adic integers for each prime p.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1992
References
REFERENCES
- 1
- Cited by


