Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-12-01T08:58:17.704Z Has data issue: false hasContentIssue false
  • English
  • Français

Power-collapsing games

Published online by Cambridge University Press:  12 March 2014

Miloš S. Kurilić  and
Boris Šobot
Miloš S. Kurilić
Affiliation:
Department of Mathematics and Informatics, University of Novi Sad, Trg Dositeja Obradovića 4, 21000 Novi Sad, Serbia, E-mail: [email protected]
Boris Šobot
Affiliation:
Department of Mathematics and Informatics, University of Novi Sad, Trg Dositeja Obradovića 4, 21000 Novi Sad, Serbia, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The game 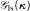is played on a complete Boolean algebra , by two players. White and Black, in κ-many moves (where κ is an infinite cardinal). At the beginning White chooses a non-zero element p ∈ . In the α-th move White chooses pα ∈ (0, p) and Black responds choosing iα ∈{0, 1}. White winsthe play iff 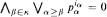. where 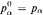and .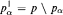

The corresponding game theoretic properties of c.B.a.'s are investigated. So, Black has a winning strategy (w.s.) if κ ≥ π() or if contains a κ-closed dense subset. On the other hand, if White has a w.s., then κ ∈ 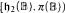. The existence of w.s. is characterized in a combinatorial way and in terms of forcing. In particular, if 2<κ = κ ∈ Reg and forcing by preserves the regularity of κ, then White has a w.s. iff the power 2κ is collapsed to κ in some extension. It is shown that, under the GCH, for each set S ⊆ Reg there is a c.B.a. such that White (respectively. Black) has a w.s. for each infinite cardinal κ ∈ S (resp. κ ∉ S). Also it is shown consistent that for each κ ∈ Reg there is a c.B.a. on which the game 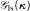is undetermined.

Keywords

Boolean algebrasgamesSuslin treesforcing
Type
Research Article
Information
The Journal of Symbolic Logic , Volume 73 , Issue 4 , December 2008 , pp. 1433 - 1457
Copyright
Copyright © Association for Symbolic Logic 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Dobrinen, N., Games and generalized distributive laws in Boolean algebras, Proceedings of the American Mathematical Society, vol. 131 (2003), no. 1, pp. 309–318.CrossRefGoogle Scholar
[2]Dobrinen, N., Errata to “Games and generalized distributive laws in Boolean algebras”, Proceedings of the American Mathematical Society, vol. 131 (2003), no. 9, pp. 2967–2968.CrossRefGoogle Scholar
[3]Jech, T., More game-theoretic properties of Boolean algebras, Annals of Pure and Applied Logic, vol. 26 (1984), pp. 11–29.CrossRefGoogle Scholar
[4]Jech, T., Set theory, 2nd corr. ed., Springer, Berlin, 1997.CrossRefGoogle Scholar
[5]Kunen, K., Set theory, An introduction to independence proofs, North-Holland, Amsterdam, 1980.Google Scholar
[6]Kurilić, M. S. and Šobot, B., A game on Boolean algebras describing the collapse of the continuum, submitted.Google Scholar
[7]Zapletal, J., More on the cut and choose game, Annals of Pure and Applied Logic, vol. 76 (1995), pp. 291–301.CrossRefGoogle Scholar