Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-26T22:49:53.808Z Has data issue: false hasContentIssue false
  • English
  • Français

Potential isomorphism of elementary substructures of a strictly stable homogeneous model

Published online by Cambridge University Press:  12 March 2014

Sy-David Friedman ,
Tapani Hyttinen  and
Agatha C. Walczak-Typke
Sy-David Friedman
Affiliation:
Kurt Gödel Research Center For Mathematical Logic, University of Vienna, A-1090 Vienna, Austria, E-mail: [email protected]
Tapani Hyttinen
Affiliation:
Department of Mathematics and Statistics, University of Helsinki, Fi-00014 Helsinki, Finland, E-mail: [email protected]
Agatha C. Walczak-Typke
Affiliation:
Department of Mathematics and Statistics, University of Helsinki, Fi-00014 Helsinki, Finland, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The results herein form part of a larger project to characterize the classification properties of the class of submodels of a homogeneous stable diagram in terms of the solvability (in the sense of [1]) of the potential isomorphism problem for this class of submodels.

We restrict ourselves to locally saturated submodels of the monster model 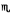, of some power π. We assume that in Gödel's constructive universe 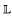, π is a regular cardinal at least the successor of the first cardinal in which 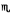, is stable.

We show that the collection of pairs of submodels in 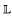as above which are potentially isomorphic with respect to certain cardinal-preserving extensions of 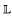is equiconstructible with 0#. As 0# is highly “transcendental” over 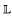, this provides a very strong statement to the effect that potential isomorphism for this class of models not only fails to be set-theoretically absolute, but is of high (indeed of the highest possible) complexity.

The proof uses a novel method that does away with the need for a linear order on the skeleton.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 76 , Issue 3 , September 2011 , pp. 987 - 1004
Copyright
Copyright © Association for Symbolic Logic 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Friedman, Sy D., Cardinal-preserving extensions, this Journal, vol. 68 (2003), no. 4, pp. 1163–1170.Google Scholar
[2]Friedman, Sy David, Hyttinen, Tapani, and Rautila, Mika, Classification theory and 0#, this Journal, vol. 68 (2003), no. 2, pp. 580–588.Google Scholar
[3]Grossberg, Rami and Lessmann, Olivier, Shelah's stability spectrum and homogeneity spectrum infinite diagrams, Archive for Mathematical Logic, vol. 41 (2002), no. 1, pp. 1–31.CrossRefGoogle Scholar
[4]Grossberg, Rami and Shelah, Saharon, On the number of nonisomorphic models of an infinitary theory which has the infinitary order property. Part A, this Journal, vol. 51 (1986), no. 2, pp. 302–322.Google Scholar
[5]Huuskonen, Taneli, Hyttinen, Tapani, and Rautila, Mika, On potential isomorphism and non-structure, Archive for Mathematical Logic, vol. 43 (2004), no. 1, pp. 85–120.Google Scholar
[6]Hyttinen, Tapani, On nonstructure of elementary submodels of an unsuperstable homogeneous structure, Mathematical Logic Quarterly, vol. 43 (1997), no. 1, pp. 134–142.CrossRefGoogle Scholar
[7]Hyttinen, Tapani, A short introduction to classification theory, Graduate Texts in Mathematics, vol. 2, Department of Mathematics, University of Helsinki, Helsinki, 1997.Google Scholar
[8]Hyttinen, Tapani and Shelah, Saharon, On the number of elementary submodels of an unsuperstable homogeneous structure, Mathematical Logic Quarterly, vol. 44 (1998), pp. 354–358.CrossRefGoogle Scholar
[9]Hyttinen, Tapani and Shelah, Saharon, Strong splitting in stable homogeneous models, Annals of Pure and Applied Logic, vol. 103 (2000), no. 1–3, pp. 201–228.CrossRefGoogle Scholar
[10]Hyttinen, Tapani and Shelah, Saharon, Main gap for locally saturated elementary submodels of a homogeneous structure, this Journal, vol. 66 (2001), no. 3, pp. 1286–1302.Google Scholar
[11]Hyttinen, Tapani and Tuuri, Heikki, Constructing strongly equivalent nonisomorphic models for unstable theories, Annals of Pure and Applied Logic, vol. 52 (1991), no. 3, pp. 203–248.CrossRefGoogle Scholar
[12]Jech, Thomas, Set theory, the third millennium, revised and expanded ed., Springer Monographs in Mathematics, Springer-Verlag, Berlin, 2003, xiv + 769.Google Scholar
[13]Shelah, Saharon, Finite diagrams stable in power, Annals of Mathematical Logic, vol. 2 (1970), pp. 69–118.CrossRefGoogle Scholar
[14]Shelah, Saharon, Existence of many L∞,λ-equivalent, nonisomorphic models of T of power λ, Annals of Pure and Applied Logic, vol. 34 (1987), pp. 291–310.CrossRefGoogle Scholar
[15]Shelah, Saharon, Classification theory and the number of non-isomorphic models, 2nd revised ed., Studies in Logic and the Foundations of Mathematics, vol. 92, North-Holland, Amsterdam, 1990.Google Scholar