Article contents
A polarized partition relation for weakly compact cardinals using elementary substructures
Published online by Cambridge University Press: 12 March 2014
Abstract
We show that if κ is a weakly compact cardinal, then
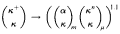
for any ordinals α < κ+ and μ < κ, and any finite ordinals m and n. This polarized partition relation represents the statement that for any partition
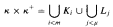
of κ × κ+ into m + μ pieces either there are A ∈ [κ]κ, B ∈ [κ]+]α and i < m with A × B ⊆ Ki or there are C ∈ [κ]κ, 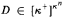 , and j < μ with C × D ⊆ Lj. Related results for measurable and almost measurable κ are also investigated. Our proofs of these relations involve the use of elementary substructures of set models of large fragments of ZFC.
, and j < μ with C × D ⊆ Lj. Related results for measurable and almost measurable κ are also investigated. Our proofs of these relations involve the use of elementary substructures of set models of large fragments of ZFC.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2006
References
REFERENCES
- 2
- Cited by


