Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T12:59:40.591Z Has data issue: false hasContentIssue false
  • English
  • Français

Périodicité des théories élémentaires des corps de séries formelles itérées

Published online by Cambridge University Press:  12 March 2014

Françoise Delon
Françoise Delon*
Affiliation:
Équipe de Logique Mathématique, Université Paris VII, Paris, France
Get access Rights & Permissions [Opens in a new window]

Abstract

C. U. Jensen suggested the following construction, starting from a field K:

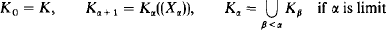
and asked when two fields Kα and Kβ are equivalent. We give a complete answer in the case of a field K of characteristic 0.

Keywords

Ax/Kochen-Eršov theoremdefinability of valuations in the language of ringselementary equivalenceelementary inclusionfirst-order theoriesiterated power series fieldsgeneralized power series fieldsperiodicity.
Type
Research Article
Information
The Journal of Symbolic Logic , Volume 51 , Issue 2 , June 1986 , pp. 334 - 351
Copyright
Copyright © Association for Symbolic Logic 1986

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

RÉFÉRENCES

[A] Ax, J., On the undecidability of power series fields, Proceedings of the American Mathematical Society, vol. 16 (1965), p. 846.Google Scholar
[CK] Chang, C. C. and Keisler, H. J., Model theory, North-Holland, Amsterdam, 1973.Google Scholar
[D] Delon, F., Corps équivalents à leur corps de séries, Logique (Conférence, Paris, 1983; F. Delon et al, éditeurs), Mémoire de la Société Mathématique de France, Nouvelle Série, Tome 16, Bordas, Paris, 1984, pp. 95–103.Google Scholar
[DMT] Doner, J., Mostowski, A. and Tarski, A., The elementary theory of well-ordering—a metamathematical study, Logic Colloquium '77, North-Holland, Amsterdam, 1978, pp. 1–54.Google Scholar
[DT] Doner, J. and Tarski, A., Extended arithmetic of ordinal numbers, Fundamenta Mathematicae, vol. 65 (1969), pp. 95–127.CrossRefGoogle Scholar
[EE] Endler, O. and Engler, A. J., Fields with Henselian valuation rings, Mathematische Zeitschrift, vol. 152 (1977), pp. 191–193.CrossRefGoogle Scholar
[FV] Feferman, S. and Vaught, R., The first order properties of products of algebraic systems, Fundamenta Mathematicae, vol. 47 (1959), pp. 57–103.CrossRefGoogle Scholar
[G1] Gurevich, Y., Elementary properties of ordered Abelian groups, American Mathematical Society Translations, ser. 2, vol. 46 (1965), pp. 165–192.Google Scholar
[G2] Gurevich, Y., Expanded theory of Abelian groups, Annals of Mathematical Logic, vol. 12 (1977), pp. 193–228.CrossRefGoogle Scholar
[KK ] Kreisel, G. et Krivine, J. L., Eléments de logique mathématique, Dunod, Paris, 1967.Google Scholar
[MT] Mostowski, A. and Tarski, A., Arithmetical classes and types of well ordered systems, Bulletin of the American Mathematical Society, vol. 55 (1949), p. 65.Google Scholar
[O] Oger, F., Produits lexicographiques de groupes ordonnés: Isomorphisme et équivalence élémentaire, Journal of Algebra (à paraitre).Google Scholar
[R] Ribenboïm, P., Théorie des valuations, Les Presses de l'Université de Montréal, Montréal, 1964.Google Scholar
[S1] Schmitt, P., Elementary properties of ordered Abelian groups (to appear).Google Scholar
[S2] Schmitt, P., Model theory of ordered Abelian groups, Habilitationsschrift, Heidelberg, 1982.Google Scholar