Article contents
Paradox of the class of all grounded classes
Published online by Cambridge University Press: 12 March 2014
Extract
A class A for which there is an infinite progression of classes A1, A2, … (not necessarily all distinct) such that
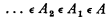
is said to be groundless. A class which is not groundless is said to be grounded. Let K be the class of all grounded classes.
Let us assume that K is a groundless class. Then there is an infinite progression of classes A1, A2, … such that
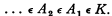
Since A1 ϵ K, A1 is a grounded class; since
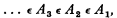
A1 is also a groundless class. But this is impossible.
Therefore K is a grounded class. Hence K ϵ K, and we have
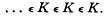
Therefore K is also a groundless class.
This paradox forms a sort of triplet with the paradox of the class of all non-circular classes and the paradox of the class of all classes which are not n-circular (n a given natural number). The last of the three includes as a special case the paradox of the class of all classes which are not members of themselves (n = 1).
More exactly, a class A1 is circular if there exists some positive integer n and classes A2, A3, …, An such that
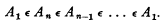
For any given positive integer n, a class A1 is n-circular if there are classes A2, …, An, such that
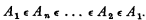
Quite obviously, by arguments similar to the above, we get a paradox of the class of all non-circular classes and a paradox of the class of all classes which are not n-circular, for each positive integer n.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1953
References
1 The referee pointed out that on pp. 128–130 of Mathematical logic (revised ed., 1951, Cambridge, Mass., U.S.A.)Google Scholar, W. V. Quine proves a result (his *181) which amounts to the same thing as the paradox of the class of all classes which are not n-circular.
- 14
- Cited by


