Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-19T17:05:15.939Z Has data issue: false hasContentIssue false
  • English
  • Français

Open induction and the true theory of rationals

Published online by Cambridge University Press:  12 March 2014

Zofia Adamowicz
Zofia Adamowicz*
Affiliation:
Institute of Mathematics, Polish Academy of Sciences, Warsaw, Poland
Get access Rights & Permissions [Opens in a new window]

Extract

In the paper we prove the following theorem:

Theorem. There is a model N of open induction in which the set of primes is bounded and N is such that its field of fractions 〈N*, +, ·, <〉 is elementarily equivalent to 〈Q, +, ·, <〉 (the standard rationals).

We fix an ω 1-saturated model 〈M, +, ·, <〉 of PA. Let 〈M*, +, ·, <〉 denote the field of fractions of M. The model N that we are looking for will be a substructure of 〈M*, +, ·, <〉.

If A ⊆ M* then let Ā denote the ring generated by A within M*, Ậ the real closure of A, and A* the field of fractions generated by A. We have

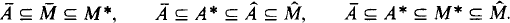
Let J ⊆ M. Then 〈M*, +, ·〉 is a linear space over J*. If x 1,…,xk ∈ M*, we shall say that x 1,…,xk are J-independent if 〈1, x 1,…, xk 〉 are J*-independent in the usual sense. As usual, we extend the notion of J-independence to the case of infinite sets.

If A ⊆ M* and X ⊆ A, then we say that X is a J-basis of A if X is a maximal subset of A which is J-independent.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 52 , Issue 3 , September 1987 , pp. 793 - 801
Copyright
Copyright © Association for Symbolic Logic 1987

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Shepherdson, J. C., A non-standard model for a free variable fragment of number theory, Bulletin de l'Académie Polonaise des Sciences, Série des Sciences Mathématiques, Astronomiques et Physiques, vol. 12 (1964), pp. 79–86.Google Scholar
[2] Wilkie, A. J., Some results and problems on weak systems of arithmetic, Logic Colloquium '77 (Macintyre, A. et al, editors), North-Holland, Amsterdam, 1978, pp. 285–296.CrossRefGoogle Scholar
[3] van den Dries, L., Some model theory and number theory for models of weak systems of arithmetic, Model theory of algebra and arithmetic (Proceedings, Karpacz, 1979), Lecture Notes in Mathematics, vol. 834, Springer-Verlag, Berlin, 1980, pp. 346–362.CrossRefGoogle Scholar