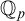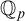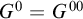ONE-DIMENSIONAL SUBGROUPS AND CONNECTED COMPONENTS IN NON-ABELIAN p-ADIC DEFINABLE GROUPS

Abstract

We generalize two of our previous results on abelian definable groups in p-adically closed fields [12, 13] to the non-abelian case. First, we show that if G is a definable group that is not definably compact, then G has a one-dimensional definable subgroup which is not definably compact. This is a p-adic analogue of the Peterzil–Steinhorn theorem for o-minimal theories [16]. Second, we show that if G is a group definable over the standard model $\mathbb {Q}_p$, then $G^0 = G^{00}$. As an application, definably amenable groups over $\mathbb {Q}_p$ are open subgroups of algebraic groups, up to finite factors. We also prove that $G^0 = G^{00}$ when G is a definable subgroup of a linear algebraic group, over any model.

1 Introduction

This paper continues our earlier work [12, 13] on definable groups in the theory $p\text {CF}$ of p-adically closed fields. We prove two main results. The first is as follows:

Theorem 1.1. Let G be a definable group in a p-adically closed field. If G is not definably compact, then G contains a one-dimensional definable subgroup H which is not definably compact.

See Sections 2.1 and 2.2 for definitions of the relevant terms. The analogous statement for definable groups in o-minimal structures is the classic Peterzil–Steinhorn theorem [16]. The abelian case of Theorem 1.1 was the main result of [12].

Our second main result concerns the model-theoretic connected components $G^0$ and $G^{00}$ . Recall that if G is a definable group in a monster model of an NIP theory such as pCF, then the collection of definable (resp. type-definable) subgroups of finite (resp. bounded) index is bounded, and the intersection is denoted $G^0$ (resp. $G^{00}$ ) [22, Section 8.1]. We always have $G^{00} \subseteq G^0$ , and the inclusion can be strict. For example, if G is the circle group in RCF, then $G^0 = G$ but $G^{00}$ is an infinitesimal neighborhood of the identity element. Our second main theorem shows that this does not happen for groups definable over $\mathbb {Q}_p$ :

Theorem 1.2. Let $\mathbb {K}$ be a highly saturated elementary extension of $\mathbb {Q}_p$ and let G be a $\mathbb {Q}_p$ -definable group in $\mathbb {K}$ . Then $G^0 = G^{00}$ .

We previously proved the abelian case in [13, Theorem 4.2]. The main goal of the current note, then, is to deal with the non-abelian cases of Theorems 1.1 and 1.2.

In the course of proving Theorem 1.2, we need to prove the following variant, which is interesting in its own right:

Theorem 1.3. Let $\mathbb {K}$ be a highly saturated p-adically closed field, let G be a linear algebraic group over $\mathbb {K}$ , and let $H \subseteq G(\mathbb {K})$ be a definable subgroup. Then $H^0 = H^{00}$ .

The assumption that G is a linear algebraic group is essential; Onshuus and Pillay show that $E(\mathbb {K})^0 \ne E(\mathbb {K})^{00}$ for certain elliptic curves [15, Proposition 3.7].

As in [13], Theorem 1.2 implies the following weak classification of definably amenable groups over $\mathbb {Q}_p$ :

Theorem 1.4. Let G be a definably amenable group defined in $\mathbb {Q}_p$ . There is a finite index definable subgroup $E \subseteq G$ and a finite normal subgroup $F \lhd E$ such that the quotient $E/F$ is isomorphic to an open subgroup of an algebraic group over $\mathbb {Q}_p$ .

Remark 1.5. Tracing through the proofs of Theorems 1.2 and 1.3, one can see that in p-adically closed fields, instances of $G^0 \ne G^{00}$ must be built out of primitive instances G for which (1) G is abelian, (2) G is not $\mathbb {Q}_p$ -definable, and (3) G is not a definable subgroup of a linear algebraic group. These constraints might be strong enough that one could classify all such groups, perhaps using the techniques of [1]. This would lead to a better understanding of the structure of $G/G^{00}$ for general definable groups G in pCF.

Remark 1.6. The term “p-adically closed field” is often used for the more general class of fields elementarily equivalent to finite extensions $K/\mathbb {Q}_p$ . All of our theorems generalize to this broader context. For simplicity we will only consider the case of $\operatorname {Th}(\mathbb {Q}_p)$ . In most cases, the proofs generalize with minimal changes. We leave the details as an exercise to the reader. However, in Section 5, some of the intermediate lemmas fail to generalize, as explained in Remark 5.1. Nevertheless, the main theorems do successfully generalize, for reasons explained in Remark 5.14.

1.1 Notation and conventions

Let $\mathcal {L}$ be a first-order language and M be an $\mathcal {L}$ -structure. The letters $x, y, z$ will denote finite tuples of variables, and $a, b, c$ will denote finite tuples from M. For a subset A of M, $\mathcal {L}_A$ is the language obtained from $\mathcal {L}$ by adjoining constants for elements of A. For an $\mathcal {L}_M$ -formula $\phi (x)$ , $\phi (M)$ denotes the definable subset of $M^{|x|}$ defined by $\phi $ . A set X is definable in M if there is an $\mathcal {L}_M$ -formula $\phi (x)$ such that $X = \phi (M)$ . If $M\prec N$ , and $X\subseteq M^n$ is defined by a formula $\psi $ with parameters from M, then $X(N)$ will denote the definable set $\psi (N)$ . We will distinguish between definable and interpretable in the current paper.

1.2 Outline

In Section 2, we review the notions of definable compactness, p-adic definable groups, and p-adic algebraic groups, as well as some useful tools. In Section 3, we prove Theorem 1.1, the p-adic Peterzil–Steinhorn theorem. In Section 4, we collect some useful information on compact Hausdorff groups and apply it to the groups $G/G^{00}$ . Finally, in Section 5 we use this machinery to prove Theorems 1.2 and 1.3.

2 Preliminaries

2.1 Definable compactness

We recall some notions from [9]. Let M be an arbitrary structure. A definable topology on a definable set $X \subseteq M^n$ is a topology with a (uniformly) definable basis of opens. A definable topological space is a definable set with a definable topology. A definable topological space X is definably compact if for any definable family ${\cal F}=\{Y_t \mid t\in T\}$ of non-empty closed sets $Y_t\subseteq X$ , if ${\cal F}$ is downwards directed, then $\bigcap {\cal F}\neq \emptyset $ . A definable subset $D \subseteq X$ is definably compact if it is definably compact as a subspace.

Fact 2.1 [9, Section 3.1].

1. 1. If X is a compact definable topological space, then X is definably compact.

2. 2. If $f :X\to Y$ is definable and continuous, and X is definably compact, then the image $f(X)\subseteq Y$ is definably compact.

3. 3. If X is definably compact and $Y\subseteq X$ is closed and definable, then Y is definably compact.

4. 4. If X is Hausdorff and $Y \subseteq X$ is definable and definably compact, then Y is closed.

5. 5. If $X_1, X_2$ are definably compact spaces, then $X_1 \times X_2$ is definably compact.

6. 6. If X is a definable topological space and $Y_1, Y_2\subseteq X$ are definably compact, then $Y_1\cup Y_2$ is definably compact.

Remark 2.2. Suppose X is a definable topological space in a structure M, and $N \succ M$ . Then $X(N)$ is naturally a definable topological space in the structure N, and $X(N)$ is definably compact if and only if X is definably compact. In other words, definable compactness is invariant in elementary extensions.

2.2 $p\text {CF}$ and definable groups

Let p be a prime and $\mathbb {Q}_p$ the field of p-adic numbers. We call the complete theory of $\mathbb {Q}_p$ , in the language of rings, the theory of p-adically closed fields, written $p\text {CF}$ . For any $K\models p\text {CF}$ , $\mathcal {O}(K)$ will denote the valuation ring and $\Gamma _K$ will denote the value group, which is an elementary extension of $(\mathbb {Z},+,<)$ . Let $v: K\to \Gamma _K\cup \{\infty \}$ be the valuation map and

$$\begin{align*}B(a, \alpha) = \{x \in \mathbb{Q}_p \mid v(x-a)\geq \alpha\} \end{align*}$$

for $a\in K$ and $\alpha \in \Gamma _K\cup \{\infty \}$ . Then K is topological field with basis given by the sets $B(a, \alpha )$ . The p-adic field $\mathbb {Q}_p$ is locally compact. We call $X\subseteq K$ bounded if there is $\alpha \in \Gamma _K$ such that X is a subset of some n-dimensional ball $B(0, \alpha )^n$ .

Fact 2.3 [12, Lemmas 2.4 and 2.5].

Let X be a definable subset of $K^n$ . Then X is definably compact iff X is closed and bounded.

An n-dimensional definable $C^k$ -manifold over K is a Hausdorff definable topological space X with a finite covering by open sets each homeomorphic to an open definable subset of $K^{n}$ with transition maps definable and $C^{k}$ .

By a definable group over K, we mean a definable set with a definable group operation. By adapting the methods of [17] one sees that for any group G definable in K and for any $k<\omega $ , G can be definably equipped with the structure of a definable $C^{k}$ -manifold in K with respect to which the group structure is $C^{k}$ . Moreover, this $C^k$ -manifold structure is unique. We will always use this manifold structure when making topological statements about G. For example, G is “definably compact” if it is definably compact with respect to this $C^k$ -manifold structure.

As observed in Proposition 2.1 of [8], p-adically closed fields are geometric fields, in the sense that (1) they have uniform finiteness and (2) model-theoretic algebraic closure agrees with field-theoretic algebraic closure:

$$ \begin{align*} a \in \operatorname{acl}(F) \iff a \in F^{\mathrm{alg}}. \end{align*} $$

Consequently, there is a sensible dimension theory for definable sets. Assuming $X\subseteq K^n$ is definable over a set A, then the dimension $\dim (X)$ can be described as the maximum of $\dim (\bar a/A)$ as $\bar a$ ranges over points of $X(N)$ , where N is an $|A|^+$ -saturated elementary extension of K. The dimension $\dim (X)$ coincides with the algebro-geometric dimension of the Zariski closure of X.

2.3 Algebraic groups

Let K be a p-adically closed field and L be an algebraically closed field containing K. Let G be an algebraic group definable in L, with parameters from K, which means that the variety structure as well as the group structure are given by data over K (see [18] for more details). Then G and its group operation are defined by quantifier-free formulas over K in the language of rings. The K-points $G(K)$ of the algebraic group G is of course a definable group in K. By a “definable subgroup of an algebraic group,” we mean a definable subgroup of $G(K)$ for some algebraic group G.

2.4 Centralizer-connected groups

Let $(G,\cdot )$ be a definable group in a p-adically closed field K. The following definition is standard:

Definition 2.4. G is centralizer-connected if there is no $a \in G$ such that the centralizer $Z_G(a)$ is a proper subgroup of G of finite index.

The proofs of the next two theorems are variants of the proof of [19, Proposition 2.3].

Theorem 2.5. Let $G'$ be the intersection of all finite-index centralizers in G. Then $G'$ is a definable subgroup of finite index in G. Moreover, $G'$ is centralizer-connected.

Proof Recall that G acts on itself via conjugation, $Z_G(a)$ is the stabilizer of a, and the orbit of a is the conjugacy class $a^G$ . Thus the index of $Z_G(a)$ in G is the size of $a^G$ , and $Z_G(a)$ has finite index if and only if $a^G$ is finite. The theory of p-adically closed fields has uniform finiteness, so there is some n such that

$$ \begin{align*} |a^G| < \infty \implies |a^G| \le n \end{align*} $$

for every $a \in G$ . Equivalently,

$$ \begin{align*} |G : Z_G(a)| < \infty \implies |G : Z_G(a)| \le n. \end{align*} $$

In an NIP theory such as pCF, if G is a definable group and $\phi (x,y)$ is a formula and n is an integer, then the family

$$ \begin{align*} \{H :~ & H \text{ is a subgroup of } G,\\ & H \text{ is defined by } \phi(x,b) \text{ for some } b, \\ & \text{and } |G : H| \le n\} \end{align*} $$

is finite. ¹ Consequently, once we have a uniform bound n on the index of finite-index centralizers, it follows that there are only finitely many finite-index centralizers. Thus, the group $G' = \bigcap \{Z_G(a) : a \in G, ~ |G : Z_G(a)| < \infty \}$ is definable and has finite index.

Next, suppose that $G'$ fails to be centralizer-connected, witnessed by some element $a \in G'$ such that

$$ \begin{align*} 1 < |G' : Z_{G'}(a)| < \infty. \end{align*} $$

Then $Z_{G'}(a)$ has finite index in $G'$ , which has finite index in G. As $Z_G(a)$ contains $Z_{G'}(a)$ , we see that $Z_G(a)$ also has finite index in G. Then $G' \subseteq Z_G(a)$ by choice of $G'$ , implying that every element of $G'$ commutes with a. This makes ${Z_{G'}(a) = G'}$ .

Theorem 2.6. Suppose $(G,\cdot )$ is centralizer-connected and non-abelian.

1. 1. $\dim (Z_G(a)) < \dim (G)$ for every $a \in G \setminus Z(G)$ .

2. 2. $\dim (Z(G)) < \dim (G)$ .

Proof

1. 1. There is an interpretable bijection between the conjugacy class $a^G$ and the set of cosets $G/Z_G(a)$ . By dimension theory,

   $$ \begin{align*} \dim(G) = \dim(Z_G(a)) + \dim(a^G). \end{align*} $$
   Suppose that $\dim (Z_G(a)) = \dim (G)$ for the sake of contradiction. Then $\dim (a^G) = 0$ , implying that $a^G$ is finite and $Z_G(a)$ has finite index in G. As G is centralizer-connected, $Z_G(a) = G$ . But then $a \in Z(G)$ .

2. 2. Take any $a \in G \setminus Z(G)$ . Then $Z(G) \subseteq Z_G(a)$ , so $\dim (Z(G)) \le \dim (Z_G(a)) < \dim (G)$ .

We will also need the following related facts from [19]:

Fact 2.7. Let G be a group definable in K. If G has a commutative open neighborhood of the identity, then G is commutative-by-finite.

Fact 2.8. Let G be a group definable in K. If $\dim (G) = 1$ , then G is commutative-by-finite.

2.5 “Affine” groups and the adjoint action

Let K be a p-adically closed field. Let G be a group definable in K of dimension n. For $g\in G$ the map $\operatorname {Inn}(g): x\mapsto gxg^{-1}$ is a $C^k$ automorphism of G and thus has a differential $d(\operatorname {Inn}(g))_{1}$ at the identity $1 \in G$ . The differential $d(\operatorname {Inn}(g))_1$ is a linear map on the tangent space $T_1 G \to T_1 G$ . The map $\operatorname {Ad}: g \mapsto d(\operatorname {Inn}(g))_{\operatorname {id}_G}$ is a definable group homomorphism from G to $\operatorname {GL}(T_1 G)$ , called the adjoint representation of G.

Theorem 2.9. Suppose $\operatorname {Ad} : G \to \operatorname {GL}(T_1 G)$ is trivial.

1. 1. There is a commutative open neighborhood U of $1 \in G$ .

2. 2. G is commutative-by-finite.

Proof By Fact 2.7, it suffices to prove part (1). The statement of (1) can be expressed via infinitely-many first-order sentences, so we may assume that $K = \mathbb {Q}_p$ . Then G is a p-adic Lie group. By [21, Corollary 18.18], it suffices to show that the Lie algebra of G is abelian, i.e., trivial. ² That is, we must show that $[s,t] = 0$ for $s, t \in \operatorname {Lie}(G)$ .

The correct way to see this is to apply the functor $\operatorname {Lie}(-)$ from Lie groups to Lie algebras to the morphism $\operatorname {Ad} : G \to \operatorname {GL}(T_1 G)$ . The result is known to be the adjoint representation

$$ \begin{align*} \operatorname{ad} : \operatorname{Lie}(G) &\to \mathfrak{gl}(\operatorname{Lie}(G)) \\ \operatorname{ad}(s) &= [s,-] \end{align*} $$

(though we had trouble finding a reference for this fact in the p-adic Lie group setting). The triviality of $\operatorname {Ad} : G \to \operatorname {GL}(T_1 G)$ implies triviality of $\operatorname {ad}(-)$ , which means that $[s,t] = 0$ for any s and t.

Here is a different proof. The fact that G acts trivially on the tangent space implies that any vector $s \in T_1G$ extends uniquely to a vector field $\xi _s$ on G that is both left and right invariant. Indeed, if $\lambda _g$ and $\rho _g$ denote left and right multiplication by $g \in G$ , then $\lambda _g^{-1} \circ \rho _g$ fixes s by triviality of the adjoint representation $\operatorname {Ad}(-)$ , and so $\lambda _g(s) =\rho _g(s)$ .

The Lie algebra structure on $T_1G$ is induced by the Lie algebra structure on right-invariant vector fields:

$$ \begin{align*} \xi_{[s,t]} = [\xi_s,\xi_t] \end{align*} $$

(see [21, p. 100, Definition]). However, a left-invariant vector field $\xi _1$ commutes with a right-invariant vector field $\xi _2$ , by an easy calculation related to the fact that the action of G on the left commutes with the action of G on the right. Since $\xi _s$ and $\xi _t$ are both left-invariant and right-invariant, they commute. Therefore, the Lie algebra of G is abelian.

Recall that an algebraic group G is said to be “linear” if it is an algebraic subgroup of $\operatorname {GL}_n$ for some n. Analogously,

Definition 2.10. A definable group G is affine if G is a definable subgroup of $\operatorname {GL}_n(K)$ for some n.

Perhaps “linear” would have been a better term than “affine”, but it seemed helpful to use separate terminology for the two concepts—one is a property of algebraic groups and one is a property of definable groups. At any rate, the two concepts are related as follows:

1. 1. If H is a linear algebraic group, then any definable subgroup $G \subseteq H(K)$ is an affine definable group. In other words, affine definable groups are exactly the definable subgroups of linear algebraic groups.

2. 2. If $G \subseteq GL_n(K)$ is an affine definable group, then the Zariski closure of G in $\operatorname {GL}_n$ is a linear algebraic group.

Note that Theorem 1.3 is a statement about affine definable groups.

Lemma 2.11. If G is a definable group in K, then there is a definable short exact sequence of K-definable groups

$$\begin{align*}1\rightarrow A\rightarrow G\stackrel{\pi}{\rightarrow} H\rightarrow 1, \end{align*}$$

where A is commutative-by-finite, and H is an affine group.

Proof Consider the adjoint representation $\operatorname {Ad}: G\rightarrow \operatorname {GL}(T_1 G)$ of G. Let $\pi =\operatorname {Ad}$ , $A=\ker (\operatorname {Ad})$ , and $H=\operatorname {im}(\operatorname {Ad})$ . Note that the adjoint action of A is trivial, and so A is commutative-by-finite by Theorem 2.9.

2.6 Definable compactness in extensions and quotients

Let G be a definable group in a p-adically closed field K, and let H be a definable subgroup. As noted above, G and H have the structure of definable manifolds, making them into topological groups.

Fact 2.12 [11, Section 5.4].

The inclusion of H into G is a closed embedding, and a clopen embedding if $\dim (H) = \dim (G)$ .

In particular, if G is a definable group and H is a definable subgroup of the same dimension, then H is clopen as a subset of G.

Corollary 2.13. If H has finite index in G, then H is definably compact if and only if G is definably compact.

Proof The groups H and G have the same dimension, so H is a clopen subgroup of G. Then G is homeomorphic to the disjoint union of finitely many copies of H.

Moving beyond the finite-index case, regard the interpretable set $G/H$ as a topological space using the quotient topology. By the argument of [13, Proposition 5.1], the continuous map $G \to G/H$ is an open map and the quotient topology is definable—or rather, interpretable. Consequently, it makes sense to say that $G/H$ is or isn’t definably compact.

Theorem 2.14. The group G is definably compact if and only if H and $G/H$ are definably compact.

Proof First suppose G is definably compact. By Fact 2.12, H is a closed subspace of G, and so H is definably compact. The continuous surjection $G \to G/H$ shows that $G/H$ is definably compact.

Conversely, suppose that H and $G/H$ are definably compact. By Proposition 2.8 in [12], there is a definable family of sets $\{U_\gamma \}_{\gamma \in \Gamma }$ such that (1) each $U_\gamma $ is open and definably compact, (2) the family is increasing in the sense that

$$ \begin{align*} \gamma \le \gamma' \implies U_\gamma \subseteq U_{\gamma'}, \end{align*} $$

and (3) $G = \bigcup _{\gamma \in \Gamma } U_\gamma $ . Let $f : G \to G/H$ be the quotient map. Because f is a continuous open map, each set $f(U_\gamma )$ is open and definably compact. By definable compactness of $G/H$ , there is some $\gamma $ such that $f(U_\gamma ) = G/H$ , implying that $G \subseteq U_\gamma \cdot H$ . Then G is the image of the definably compact space $U_\gamma \times H$ under the continuous map $(x,y) \mapsto x \cdot y$ , so G is definably compact.

A nearly identical proof shows the following.

Theorem 2.15. If $K = \mathbb {Q}_p$ , then the group G is compact if and only if H and $G/H$ are compact.

In fact, Theorem 2.15 follows from Theorem 2.14, because definable compactness agrees with compactness for interpretable topological spaces in $\mathbb {Q}_p$ [2, Theorem 8.15], but this is overkill.

Fact 2.16 [11, Proposition 5.19].

In the case where H is a normal subgroup and the quotient $G/H$ is definable $($ rather than interpretable $)$ , the quotient topology on $G/H$ agrees with the definable manifold topology as a definable group.

Corollary 2.17. Let $1 \to A \to B \to C \to 1$ be a short exact sequence of definable groups. Regard $A, B, C$ as definable manifolds.

1. 1. The maps $A \to B$ and $B \to C$ are continuous.

2. 2. The map $A \to B$ is a closed embedding.

3. 3. The map $B \to C$ is an open map.

4. 4. B is definably compact if and only if A and C are definably compact.

3 The p-adic Peterzil–Steinhorn theorem

In this section, we will prove the following theorem.

Theorem 3.1. Let G be a group definable in a p-adically closed field K. If G is not definably compact, then G contains a one-dimensional subgroup which is not definably compact.

Let G be a group definable in K. Say that G is nearly abelian if there is a definably compact definable normal subgroup $O\subseteq G$ with $G/O$ abelian. The following was proved in [12]:

Fact 3.2. If G is not definably compact and G is nearly abelian, then there is a one-dimensional definable subgroup $H\subseteq G$ that is not definably compact.

3.1 Reduction to the standard model $\mathbb {Q}_p$

We first show that Theorem 3.1 is independent of K, by finding an equivalent condition which depends only on $\operatorname {Th}(K)$ .

Definition 3.3. Let $(G,\cdot )$ be a definable group in a p-adically closed field K.

1. 1. $(G,\cdot )$ is a counterexample if G is not definably compact, but every one-dimensional definable subgroup of G is definably compact. In other words, G is a counterexample to Theorem 3.1.

2. 2. $(G,\cdot )$ is a special counterexample if G is not definably compact, but the center $Z(G)$ is definably compact, and the centralizer $Z_G(a)$ is definably compact for any $a \in G \setminus Z(G)$ .

Lemma 3.4. If G is a special counterexample, then G is a counterexample.

Proof Otherwise, there is a one-dimensional definably non-compact subgroup $H \subseteq G$ . By Fact 2.8, there is a finite-index abelian definable subgroup $H' \subseteq H$ . Then $H'$ is not definably compact (Corollary 2.13). Replacing H with $H'$ , we may assume that H is abelian. By Corollary 2.17(4), H cannot be contained in any definably compact definable subgroups of G. In particular, $H \not \subseteq Z(G)$ . Take $a \in H \setminus Z(G)$ . Then $H \not \subseteq Z_G(a)$ , which means that H is non-abelian, a contradiction.

Lemma 3.5. If G is a counterexample and H is a definable subgroup, then H is definably compact or H is a counterexample.

Proof Any one-dimensional definably non-compact subgroup of H would be a one-dimensional definably non-compact subgroup of G.

Lemma 3.6. Let G be a definable group and H be a definable subgroup of finite index. Then H is a counterexample if and only if G is a counterexample.

Proof By Corollary 2.13, G is definably compact if and only if H is. Suppose neither group is definably compact. If C is a one-dimensional definably non-compact subgroup of H, then C is also a one-dimensional definably non-compact subgroup of G. Conversely, if C is a one-dimensional definably non-compact subgroup of G, then $C \cap H$ is a one-dimensional subgroup of H which is definably non-compact because it has finite index in C, using Corollary 2.13 again.

Theorem 3.7. For a fixed p-adically closed field K, the following are equivalent $:$

1. 1. There is a counterexample G.

2. 2. There is a special counterexample G.

Proof (2) $\implies $ (1) is Lemma 3.4. For (1) $\implies $ (2), suppose there is at least one counterexample. Take a counterexample G minimizing $\dim (G)$ . By Theorem 2.5 and Lemma 3.6, we may replace G with a finite index subgroup and assume that G is centralizer-connected. If G is abelian, then G is not a counterexample, by Fact 3.2. Therefore G is non-abelian, and Theorem 2.6 applies, showing that

$$ \begin{align*} \dim(Z(G)) < \dim(G) \ \ \qquad\qquad \\\dim(Z_G(a)) < \dim(G) \text{ for } a \in G \setminus Z(G). \end{align*} $$

Then $Z(G)$ and $Z_G(a)$ are not counterexamples, by choice of G. By Lemma 3.5, they must be definably compact, making G be a special counterexample.

Remark 3.8. Let $\{G_t\}_{t \in X}$ be a definable family of definable groups.

1. 1. The set $\{t \in X : G_t \text { is definably compact}\}$ is definable [11, Theorem 6.6].

2. 2. The set $\{t \in X : G_t \text { is a special counterexample}\}$ is definable. This follows almost immediately from the previous point.

Consequently, if $K \equiv \mathbb {Q}_p$ , then there is a special counterexample in K if and only if there is a special counterexample in $\mathbb {Q}_p$ . ³ By Theorem 3.7, K has a counterexample if and only if $\mathbb {Q}_p$ has a counterexample. Therefore, in Theorem 3.1, we may assume that $K = \mathbb {Q}_p$ .

3.2 The case of $\mathbb {Q}_p$

Now assume that K is $\mathbb {Q}_p$ . We prove Theorem 3.1 by induction on the dimension of G. The assumption that $K = \mathbb {Q}_p$ will only be used in the proof of Lemma 3.13.

Say that a definable group G is good if it is not a counterexample to Theorem 3.1, meaning that either G is definably compact, or G has a one-dimensional definably non-compact subgroup.

Lemma 3.9. Suppose that $1 \to A \to B \to C \to 1$ is a short exact sequence of definable groups, and A and C are good. Then B is good.

Proof If B is definably compact, there is nothing to prove. Suppose B is definably non-compact. If A is definably non-compact, it has a one-dimensional definably non-compact subgroup X, which shows that B is good. Otherwise, A is definably compact. Then C is definably non-compact by Corollary 2.17. As C is good, there is a one-dimensional definably non-compact subgroup $X \subseteq C$ . By Fact 2.8, we may replace X with a finite index subgroup, and assume that X is abelian. Let $X^* \subseteq B$ be the preimage of X under $B \to C$ . The short exact sequence $1 \to A \to X^* \to X \to 1$ shows that $X^*$ is definably non-compact (by Corollary 2.17) and nearly abelian (as X is abelian and A is definably compact). By the nearly abelian case (Fact 3.2), $X^*$ has a one-dimensional definably non-compact subgroup, which shows that B is good.

Lemma 3.10. Suppose that G is a definable group contained in a solvable linear algebraic group $B(\mathbb {Q}_p)$ . Then G is good $:$ if G is non-compact, then G has a one-dimensional definable subgroup which is not definably compact.

Proof Proceed by induction on the solvable length of B, the length of the derived series. If the derived length is $\le 1$ , then B and G are abelian, and G is good by the abelian case (Fact 3.2). Otherwise, there is a normal algebraic subgroup $B_1 \subseteq B$ such that the algebraic groups $C := B/B_1$ and $B_1$ have lower solvable length. Let $f : G \to C(\mathbb {Q}_p)$ be the composition

$$ \begin{align*} G \hookrightarrow B(\mathbb{Q}_p) \to C(\mathbb{Q}_p). \end{align*} $$

The kernel is $G \cap B_1(\mathbb {Q}_p)$ , which is good by induction. The image is a definable subgroup of $C(\mathbb {Q}_p)$ , which is good by induction. By Lemma 3.9, G is good.

Recall from Definition 2.10 that a definable group is affine if it is a subgroup of some linear algebraic group $G(\mathbb {Q}_p)$ . Lemma 3.10 shows that certain affine groups are good, and we next generalize this to all affine groups. But first, we need a lemma.

Lemma 3.11. Let D, H and A be topological groups, with H an open subgroup of D, and A a subgroup of D.

1. 1. In the quotient topology on $D/A$ , the subset $H/(A \cap H)$ is clopen.

2. 2. The quotient topology on $H/(A \cap H)$ as a quotient of H agrees with the subspace topology as a subspace of $D/A$ .

3. 3. If the quotient topology on $D/A$ is compact, then the quotient topology on $H/(A \cap H)$ is compact.

Proof

1. 1. Note that D acts on $D/A$ on the left, and the subset $H/(A \cap H)$ is $\{hA : h \in H\}$ , which is the H-orbit of $1A \in D/A$ . It suffices to show that every H-orbit is open, which implies then that every H-orbit is closed.

   Let $\pi : D \to D/A$ be the quotient map $\pi (x) = xA$ . For any $d \in D$ , the H-orbit of $dA {\kern-1pt}\in{\kern-1pt} D/A$ is $\{hdA {\kern-1.2pt}: h {\kern-1.2pt}\in{\kern-1.2pt} H\}$ , whose preimage under $\pi $ is $\{hda {\kern-1.2pt}: h {\kern-1.2pt}\in{\kern-1.2pt} H, a \in A\} = HdA$ . This set is open, because it is a union of right-translates of the open subgroup H. By definition of the quotient topology, $\{hdA : h \in H\}$ is open in $D/A$ .

2. 2. Let S be a subset of $H/(A \cap H)$ . Let $Q = \{h \in H : \pi (x) \in S\}$ . Then S is open in the quotient topology if and only if Q is open in H or equivalently in D. As $H/(A \cap H)$ is open in $D/A$ , S is open in the subspace topology if and only if S is open as a subset of $D/A$ , meaning that $Q' = \{d \in D : \pi (d) \in S\}$ is open. So we must show that Q is open if and only if $Q'$ is open. Note that $Q = Q' \cap H$ , and H is open, so openness of $Q'$ implies openness of Q.

   Claim 3.12. $Q' = Q \cdot A$ .

   Proof If $h \in Q$ and $a \in A$ , then $\pi (ha) = haA = hA = \pi (h) \in S$ , so $ha \in Q'$ . Conversely, suppose $d \in Q'$ . Then $\pi (d) = dA \in S$ . As $S \subseteq H/(H \cap A) = \pi (H)$ , we have $\pi (d) = \pi (h)$ for some $h \in H$ . The fact that $dA = hA$ means that $d = ha$ for some $a \in A$ . Also, $\pi (h) = \pi (d) \in S$ , so $h \in Q$ . Then $d = ha \in Q \cdot A$ .

   If Q is open, then $Q'$ is open, being a union of right-translates of Q.

3. 3. This follows from the previous two points—if $D/A$ is compact, then the closed subspace $H/(H \cap A)$ is compact, and this space is homeomorphic to the quotient space $H/(H \cap A)$ .

Lemma 3.13. If G is affine, then G is good.

Proof Suppose G is a definable subgroup of $V(\mathbb {Q}_p)$ for some linear algebraic group V over $\mathbb {Q}_p$ . Replacing V with the Zariski closure of G, we may assume that G is Zariski dense in V. Then G is open in $V(\mathbb {Q}_p)$ , because G and $V(\mathbb {Q}_p)$ have the same dimension as definable groups. Let B be a maximal connected K-split solvable algebraic subgroup of V. By Theorem 3.1 of [20], the quotient space $V(\mathbb {Q}_p)/B(\mathbb {Q}_p)$ is compact. By Lemma 3.11, $G/(G \cap B(\mathbb {Q}_p))$ is compact. If G is compact, then G is good. Suppose G is not compact. Theorem 2.15 shows that $G \cap B(\mathbb {Q}_p)$ is non-compact. The group $G \cap B(\mathbb {Q}_p)$ is also definably non-compact, since compactness and definable compactness agree for definable manifolds over the standard model [12, Remark 2.12].

On the other hand, $G \cap B(\mathbb {Q}_p)$ is good by Lemma 3.10, so it contains a one-dimensional non-compact definable subgroup. Then G has a one-dimensional non-compact definable subgroup, as desired.

Finally, we can complete the proof of the p-adic Peterzil–Steinhorn theorem:

Proof (of Theorem 3.1)

By Section 3.1, we may assume $K = \mathbb {Q}_p$ . Let G be a definable group in $\mathbb {Q}_p$ . Lemma 2.11 gives a short exact sequence of definable groups

$$ \begin{align*} 1 \to A \to G \to H \to 1, \end{align*} $$

where A is abelian-by-finite and H is affine. The group A is good by the abelian case (Fact 3.2, together with Lemma 3.6), and the group H is good by the affine case (Lemma 3.13). Then G is good by Lemma 3.9.

4 Compact Hausdorff groups and $G/G^{00}$

In this section, we review some facts about compact Hausdorff groups, and apply them to the groups $G/G^{00}$ .

Fact 4.1.

1. 1. A compact Hausdorff group G is profinite if and only if G is totally disconnected [7, Theorem 1.34].

2. 2. If G is profinite and $f : G \to H$ is a continuous surjection onto another compact Hausdorff group H, then H is profinite [7, Exercise E1.13].

3. 3. If G is a compact Hausdorff group, then the family of continuous homomorphisms from G to the orthogonal groups $\mathrm {O}(2), \mathrm {O}(3), \ldots $ separates points [7, Corollary 2.28].

4. 4. Any closed, compact subgroup of $\mathrm {O}(n)$ is a compact Lie group [7, Corollary 2.40 and Definition 2.41].

5. 5. Any profinite compact Lie group is finite [7, Exercise E2.8].

6. 6. If G is a non-discrete compact Lie group, then G has a non-trivial one-parameter subgroup, meaning a non-trivial continuous homomorphism $\mathbb {R} \to G$ [7, Theorem 5.41(iv)] $($ see also Definition 5.7 and Proposition 5.33 $($ iv $)$ in [7] $)$ .

Corollary 4.2. Let $1 \to A \to B \to C \to 1$ be a continuous short exact sequence of compact Hausdorff groups. Then B is profinite if and only if A and C are profinite.

Proof If B is profinite, then C is profinite by Fact 4.1(2), B is totally disconnected by Fact 4.1(1), the subspace A is totally disconnected, and then A is profinite by Fact 4.1(1).

Conversely, suppose A and C are profinite, or equivalently, totally disconnected. Any connected component $X \subseteq B$ maps onto a connected set in C, which must be a single point. Then X is contained in a coset of A, but each such coset is totally disconnected because A is. Therefore X is a point, and B is totally disconnected, hence profinite.

Corollary 4.3. Let G be a compact Hausdorff group. Then G is profinite if and only if every continuous homomorphism $f : G \to \mathrm {O}(n)$ has finite image.

Proof If G is profinite and $f : G \to \mathrm {O}(n)$ is a continuous homomorphism, then the image is profinite by Fact 4.1(2), a compact Lie group by (4), and finite by (5).

Conversely, suppose every continuous homomorphism from G to an orthogonal group has finite image. Let $\{f_i\}_{i \in I}$ enumerate all continuous homomorphisms $f_i : G \to \mathrm {O}(n_i)$ . By assumption, $\operatorname {im}(f_i)$ is finite for each i. Consider the product homomorphism

$$ \begin{align*} \prod_{i \in I} f_i : G \to \prod_{i \in I} \operatorname{im}(f_i). \end{align*} $$

By Fact 4.1(3), this map is injective, hence an embedding. Then G is a closed subgroup of the profinite group $\prod _{i \in I} \operatorname {im}(f_i)$ , so G is itself profinite.

Corollary 4.4. Let G be an infinite compact subgroup of $\mathrm {O}(n)$ . Then G contains a non-torsion element.

Proof By Fact 4.1(4), G is a compact Lie group. Since G is infinite, it is non-discrete. By Fact 4.1(6), there is a non-trivial continuous homomorphism $f : \mathbb {R} \to G$ . For $n \ge 1$ let $S_n$ be the closed subgroup

$$\begin{align*}S_n = \{t \in \mathbb{R} : f(t)^n = 1\} = \{t \in \mathbb{R} : f(nt) = 1\} = n^{-1} \ker(f).\end{align*}$$

If every element of G is torsion, then $\bigcup _{n = 1}^\infty S_n = \mathbb {R}$ , and so some $S_n$ has non-empty interior by Baire category. But then $S_n$ is a clopen subgroup of $\mathbb {R}$ , so $S_n = \mathbb {R}$ . As $S_n = n^{-1} \ker (f)$ , this implies $\ker (f) = \mathbb {R}$ , contradicting the non-triviality of f.

Recall that if G is a definable group in a highly saturated structure and $G^{00}$ exists, then the quotient $G/G^{00}$ is naturally a compact Hausdorff group with respect to the logic topology, the topology where a set $X \subseteq G/G^{00}$ is closed iff its preimage in G is type-definable. Similarly, $G/G^0$ is a compact Hausdorff group under its logic topology. The group $G^0$ is the intersection of the definable subgroups of finite index, and these correspond to the clopen subgroups of $G/G^{00}$ , so the group $G/G^0$ is precisely the maximal profinite quotient of $G/G^{00}$ . In particular, $G^0 = G^{00}$ if and only if $G/G^{00}$ is already profinite.

In light of this, we get the following corollaries of the facts above.

Corollary 4.5. Let $1 \to A \to B \to C \to 1$ be a short exact sequence of definable groups in an NIP theory. If $A^0 = A^{00}$ and $C^0 = C^{00}$ , then $B^0 = B^{00}$ .

Proof See Lemma 2.2 in [13], which assumed Corollary 4.2.

Remark 4.6. Let $A \subseteq B$ be definable groups in an NIP theory, with $|B : A| < \infty $ . Then $A^0 = A^{00}$ iff $B^0 = B^{00}$ . Indeed, the fact that B has finite index implies that $B^0 = A^0$ and $B^{00} = A^{00}$ .

Corollary 4.7. Let $\mathbb {M}$ be a monster model of an NIP $\mathcal {L}$ -theory, and let $\mathcal {L}_0$ be a sublanguage. Let G be a group definable in the reduct $\mathbb {M} \restriction \mathcal {L}_0$ . If $G^0 = G^{00}$ in $\mathbb {M}$ , then $G^0 = G^{00}$ in $\mathbb {M} \restriction \mathcal {L}_0$ .

Proof Let $H_1$ and $H_2$ be $G^{00}$ in $\mathbb {M}$ and $G^{00}$ in $\mathbb {M} \restriction \mathcal {L}_0$ , respectively. In the original structure $\mathbb {M}$ , the group $H_2$ is a type-definable subgroup of G of bounded index, so $H_2 \supseteq H_1$ . Then $G/H_2$ is a quotient of $G/H_1$ , so profiniteness of $G/H_1$ implies profiniteness of $G/H_2$ by Fact 4.1(2).

Corollary 4.8. Let G be a definable group in a monster model $\mathbb {M}$ of an NIP theory. Suppose $G^0 \ne G^{00}$ . Then there is an abelian definable subgroup $H \subseteq G$ such that $H^0 \ne H^{00}$ .

Proof The group $G/G^{00}$ isn’t profinite so there is a continuous homomorphism $f : G/G^{00} \to \mathrm {O}(n)$ with infinite image (Corollary 4.3). By Corollary 4.4, there is some $a \in \operatorname {im}(f)$ such that a isn’t torsion. Write a as $f(g)$ for some $g \in G$ . Then $f(g^n) = a^n \ne 1$ for all n. Let H be the center of the centralizer of g. Then H is an abelian definable subgroup of G and $g \in H$ . Let $f' : H/H^{00} \to \mathrm {O}(n)$ be the composition

$$ \begin{align*} H/H^{00} \to G/G^{00} \stackrel{f}{\to} \mathrm{O}(n). \end{align*} $$

Then $f'$ is a continuous homomorphism, and $f'(g) = a$ . Again, $f'(g^n) = a^n$ for all n. Then the image of $f'$ contains the infinite cyclic group $\langle a \rangle $ , and so $H/H^{00}$ isn’t profinite (Corollary 4.3).

Warning. It might appear that we can now complete the proof of Theorem 1.2 as follows. Suppose for the sake of contradiction that G is a $\mathbb {Q}_p$ -definable group G in a highly saturated elementary extension $\mathbb {K} \succeq \mathbb {Q}_p$ , and $G^0 \ne G^{00}$ . Applying Corollary 4.8 we get an abelian definable subgroup $H \subseteq G$ such that $H^0 \ne H^{00}$ , contradicting the abelian case of Theorem 1.2. But the abelian case of Theorem 1.2 was proven previously [13, Theorem 4.2].

This proof doesn’t work, because the group H from Corollary 4.8 might not be $\mathbb {Q}_p$ -definable, and then the abelian case of Theorem 1.2 won’t be applicable.

5 $G^0$ vs $G^{00}$

In this section, we verify Theorems 1.2 and 1.3 comparing $G^0$ and $G^{00}$ . Our strategy will be to first consider the expansion of pCF by restricted analytic functions. In this expansion, there are exponential and logarithm maps for abelian p-adic Lie groups, which allow us to locally identify algebraic tori with vector groups, simplifying the problem and mostly reducing to the case of vector groups. After proving the main theorems in the analytic setting, we transfer the results back to the base theory pCF via Corollary 4.7. We learned this trick from the work of Acosta López [1, Section 5]. A variant also appears in [15, Section 3].

Until Theorem 5.13, work in the following setting. Let $\mathbb {Q}_{p,\textrm {an}}$ be the expansion of $\mathbb {Q}_p$ by restricted analytic functions as in [5, Section 3]. The theory of $\mathbb {Q}_{p,\textrm {an}}$ is P-minimal [6], hence NIP. Let $\mathbb {K}$ be a monster model of $\mathbb {Q}_{p,\textrm {an}}$ .

Remark 5.1. In most of this paper, all the results trivially generalize from $\mathbb {Q}_p$ to finite extensions of $\mathbb {Q}_p$ . In this section, we really need to be working with $\mathbb {Q}_p$ rather than a finite extension. Later, however, we will generalize from $\mathbb {Q}_p$ to finite extensions (Remark 5.14).

Lemma 5.2. Let G be a definable subgroup of $(\mathbb {K}^n,+)$ . Then

$$ \begin{align*} G = \bigoplus_{i = 1}^n a_i \cdot H_i, \end{align*} $$

where $\{a_1,\ldots ,a_n\}$ is an $\mathbb {K}$ -linear basis of $\mathbb {K}^n$ , and each $H_i \in \{0,\mathcal {O},\mathbb {K}\}$ , for $\mathcal {O}$ the valuation ring.

For $n = 1$ , this was proven by Acosta López [1] (see Proposition 4.6, plus remarks above Lemma 5.2).

Proof The lemma is equivalent to a conjunction of first-order sentences, so we may replace $\mathbb {K}$ with the standard model $\mathbb {Q}_{p,\textrm {an}}$ . Definable groups are always closed ⁴ , so G is closed as a subset of $\mathbb {Q}_p^n$ . We claim that G is a $\mathbb {Z}_p$ -submodule of $\mathbb {Q}_p^n$ . It is certainly closed under addition and negation. Suppose $a \in \mathbb {Z}_p$ and $v \in G$ . Write a as $\lim _{n \to \infty } a_n$ with $a_n \in \mathbb {Z}$ . (Here we use the fact that $\mathbb {Z}$ is dense in $\mathbb {Q}_p$ , which would fail in a finite extension of $\mathbb {Q}_p$ !) Then $av = \lim _{n \to \infty } a_nv$ . Each element $a_nv$ is in G because G is a group (a $\mathbb {Z}$ -module), and then the limit $av$ is in G because G is closed.

Now proceed as in the proof of [10, Theorem 2.6], using the fact that $\mathbb {Q}_p$ is spherically complete.

Theorem 5.3. If G is a definable subgroup of $(\mathbb {K}^n,+)$ , then $G^0 = G^{00}$ .

Proof G is definably isomorphic to a direct sum of some copies of $\mathbb {K}$ and and $\mathcal {O}$ . By Corollary 4.5, we reduce to showing that $\mathbb {K}^0 = \mathbb {K}^{00}$ and $\mathcal {O}^0 = \mathcal {O}^{00}$ .

If $\mathcal {L}$ denotes the original language of $\mathbb {Q}_p$ , and $\mathcal {L}_{\textrm {an}}$ denotes the language of the expansion $\mathbb {Q}_{p,\textrm {an}}$ , then $\mathbb {K}$ and $\mathbb {K} \restriction \mathcal {L}$ have the same definable sets in one variable, because $\mathbb {Q}_{p,\textrm {an}}$ is P-minimal. Therefore, $\mathbb {K}$ and $\mathbb {K} \restriction \mathcal {L}$ also have the same type-definable sets and type-definable groups, and we can calculate the connected components $\mathbb {K}^{00}$ and $\mathcal {O}^{00}$ in the reduct $\mathbb {K} \restriction \mathcal {L}$ . In other words, we can move to the original theory pCF rather than the analytic expansion. Then it is well-known that

$$ \begin{align*} \mathbb{K}^{00} = \mathbb{K}^0 &= \mathbb{K} \\ \mathcal{O}^{00} = \mathcal{O}^0 &= \bigcap_{n = 1}^\infty p^n \mathcal{O}. \end{align*} $$

Alternatively, $\mathbb {K}^{00} = \mathbb {K}^0$ and $\mathcal {O}^{00} = \mathcal {O}^0$ hold by Theorem 4.2 in [13].

Remark 5.4. When $n = 1$ , Lemma 5.2 says that the only definable subgroups of $(\mathbb {K},+)$ are $0$ , $\mathbb {K}$ , and balls $a\mathcal {O}$ . This would fail if we were working with the theory of some finite extension $K/\mathbb {Q}_p$ rather than $\mathbb {Q}_p$ . For example, if $K = \mathbb {Q}_3(\sqrt {-1})$ , then the subring $\mathbb {Z}_3[3\sqrt {-1}] \subseteq K$ is definable, but not an $\mathcal {O}_K$ -submodule of $(K,+)$ .

On the other hand, Theorem 5.3 continues to hold, essentially because we can interpret $(K^n,+)$ as $(\mathbb {Q}_p^{dn},+)$ , for $d = [K : \mathbb {Q}_p]$ . See Remark 5.14 for the details.

Fact 5.5. If G is a definable subgroup of $(\Gamma ,+)$ , then G is $n\Gamma $ for some $0 \le n < \omega $ .

This is [1, Lemma 3.3], modulo the fact that $\Gamma $ is a pure model of Presburger arithmetic [3, Theorem 6].

Corollary 5.6. If G is a definable subgroup of $(\Gamma ,+)$ , then $G^0 = G^{00}$ .

Proof By Fact 5.5, G is trivial or isomorphic to $(\Gamma ,+)$ . In both these cases, $G^0 = G^{00}$ is known. For example, one roundabout way to see that $\Gamma ^{00} = \Gamma ^0$ is to use the fact that $\Gamma /\Gamma ^{00}$ is a quotient of $\mathbb {K}^\times /(\mathbb {K}^\times )^{00}$ by [13, Lemmas 2.1 and 2.2], and $\mathbb {K}^\times /(\mathbb {K}^\times )^{00}$ is profinite by [13, Theorem 4.2]. Then $\Gamma /\Gamma ^{00}$ is profinite by Fact 4.1(2).

Since we are working in the language with restricted analytic functions, we have exponential and logarithm maps, and we can use these to move between the multiplicative group and the additive group.

Theorem 5.7. Let G be a definable subgroup of $\mathbb {K}^\times $ . Then $G^0 = G^{00}$ .

Proof Using the short exact sequence

$$ \begin{align*} 1 \to \mathcal{O}^\times \to \mathbb{K}^\times \to \Gamma \to 1, \end{align*} $$

we can get a short exact sequence

$$ \begin{align*} 1 \to H \to G \to \Delta \to 1, \end{align*} $$

where H is a definable subgroup of $\mathcal {O}^\times $ , namely $G \cap \mathcal {O}^\times $ , and $\Delta $ is a definable subgroup of $\Gamma $ , namely $\{v(x) : x \in G\}$ . By Corollary 5.6, $\Delta ^0 = \Delta ^{00}$ . By Corollary 4.5, it remains to show that $H^0 = H^{00}$ .

If $U = 1 + p^n \mathcal {O}$ is a small enough ball around 1, then the p-adic logarithm map gives an injective definable homomorphism

$$ \begin{align*} \log_p : U \to \mathbb{Q}_p. \end{align*} $$

The index of U in $\mathcal {O}^\times $ is finite. By Remark 4.6, we may replace H with $H \cap U$ , and assume that $H \subseteq U$ . Then $H \cong \log _p(H)$ , and we are done by Theorem 5.3.

Next, we consider the case where G is a subgroup of an irreducible non-split torus.

Remark 5.8. Let T be an algebraic torus over $\mathbb {K}$ . Then T is defined over $\mathbb {Q}_p$ . Indeed, over any perfect field K of characteristic zero, n-dimensional algebraic tori are classified by actions of $\operatorname {Gal}(K)$ on $\mathbb {Z}^n$ [20, Theorem 2.1]. Boundedness of $\operatorname {Gal}(\mathbb {Q}_p)$ implies that $\operatorname {Gal}(\mathbb {K}) \cong \operatorname {Gal}(\mathbb {Q}_p)$ , and so the classification of algebraic tori is the same over both fields. More precisely, the base-change functor from tori over $\mathbb {Q}_p$ to tori over $\mathbb {K}$ is an equivalence of categories. In particular, the functor is essentially surjective, as claimed.

Remark 5.9. Let T be an irreducible non-split torus over $\mathbb {Q}_p$ . Then $T(\mathbb {Q}_p)$ is compact, by [20, Theorem 3.1].

Theorem 5.10. Let T be an irreducible non-split torus over $\mathbb {K}$ . Let G be a definable subgroup of $T(\mathbb {K})$ . Then $G^0 = G^{00}$ .

Proof By Remark 5.8, T is definable over $\mathbb {Q}_p$ . Let $n = \dim (T)$ . By properties of p-adic Lie groups, there is a neighborhood U of $1$ in $T(\mathbb {Q}_p)$ such that U is a subgroup and U is isomorphic to a ball in $\mathbb {Q}_p^n$ via an analytic logarithm map. For example, $T(\mathbb {Q}_p)$ and $\mathbb {Q}_p^n$ have isomorphic Lie algebras; apply [21, Corollary 18.18].

Therefore, there is a $\mathbb {Q}_p$ -definable open subgroup $U \subseteq T(\mathbb {K})$ and a definable injective homomorphism $\log : U \to \mathbb {K}^n$ . Note that $U(\mathbb {Q}_p)$ has finite index in $T(\mathbb {Q}_p)$ because $T(\mathbb {Q}_p)$ is compact (by Remark 5.9) and $U(\mathbb {Q}_p)$ is open. Then finitely many translates of $U(\mathbb {Q}_p)$ cover $T(\mathbb {Q}_p)$ . As $\mathbb {K} \succ \mathbb {Q}_p$ , finitely many translates of U cover $T(\mathbb {K})$ . Thus U has finite index in $T(\mathbb {K})$ . By Remark 4.6, we may replace G with the finite index subgroup $G \cap U$ , and assume that $G \subseteq U$ . Then G is definably isomorphic to a subgroup of $\mathbb {K}^n$ via the logarithm map, and so $G^0 = G^{00}$ by Theorem 5.3.

So we have seen that $G^0 = G^{00}$ when G is a definable subgroup of the additive group, the multiplicative group, or an irreducible non-split torus.

Fact 5.11. If V is a connected abelian linear algebraic group over a field K of characteristic zero, then there is a chain of algebraic subgroups (over K):

$$ \begin{align*} 1 = V_0 \subseteq V_1 \subseteq \cdots \subseteq V_n = V \end{align*} $$

such that each quotient $V_i/V_{i-1}$ is one of the following algebraic groups $:$

1. 1. The additive group $\mathbb {G}_a$ .

2. 2. The multiplicative group $\mathbb {G}_m$ .

3. 3. An irreducible non-split torus.

This follows from the fact that V is a direct product of a vector group and a torus, and a torus decomposes into irreducible tori which are either split $(\mathbb {G}_m)$ or non-split (see [14, Corollary 16.15]).

By combining Theorems 5.3, 5.7, and 5.10, we get the following:

Theorem 5.12. Let G be an affine definable group $(in\ \mathbb {K} \succ \mathbb {Q}_{p,\textrm {an}})$ . Then $G^0 = G^{00}$ .

Proof By Corollary 4.8, we may assume that G is abelian. Let V be the linear algebraic group such that $G \subseteq V(\mathbb {K})$ . Replacing V with the Zariski closure of G, we may assume that G is Zariski dense in V. Then V is abelian. By Remark 4.6, we may replace G with a finite index subgroup. Therefore, we may replace V with its connected component, and assume that V is connected.

Let $\{V_i\}_{0 \le i \le n}$ be as in Fact 5.11. For each i, consider the map

$$ \begin{align*} G \cap V_i(K) \hookrightarrow V_i(K) \to (V_i/V_{i-1})(K). \end{align*} $$

Let $G_i$ be the image. The kernel is $G \cap V_{i-1}(K)$ . Then we have an ascending chain of definable subgroups

$$ \begin{align*} 1 = G \cap V_0(K) \subseteq G \cap V_1(K) \subseteq \cdots \subseteq G \cap V_n(K) = G \end{align*} $$

such that the consecutive quotients are the definable groups $G_i \subseteq (V_i/V_{i-1})(K)$ . By Corollary 4.5, it suffices to show that $(G_i)^0 = (G_i)^{00}$ for each i. Therefore, we reduce to the case where V is one of the following:

1. 1. The additive group.

2. 2. The multiplicative group.

3. 3. An irreducible non-split torus.

These cases are handled by Theorems 5.3, 5.7, and 5.10, respectively.

Theorem 5.13. Let G be a definable group in a highly saturated elementary extension of $\mathbb {Q}_p$ . Suppose one of the following holds $:$

1. 1. G is affine.

2. 2. G is defined over $\mathbb {Q}_p$ .

Then $G^0 = G^{00}$ .

Proof

1. 1. Theorem 5.12, plus Corollary 4.7 to change the language.

2. 2. Apply Lemma 2.11 to get a $\mathbb {Q}_p$ -definable short exact sequence

   $$ \begin{align*} 1 \to A \to G \to H \to 1, \end{align*} $$
   where A is abelian-by-finite and H is affine. Then $H^0 = H^{00}$ by part (1), and $A^0 = A^{00}$ by the abelian case [13, Theorem 4.2] plus Remark 4.6. By Corollary 4.5, $G^0 = G^{00}$ .

Remark 5.14. In this section we have been working with $\mathbb {Q}_p$ rather than a finite extension $K/\mathbb {Q}_p$ . Nevertheless, Theorems 5.12 and 5.13 generalize to this setting, essentially because $K_{\textrm {an}}$ is interpretable in $\mathbb {Q}_{p,\textrm {an}}$ via a $\mathbb {Q}_p$ -linear map $K \cong \mathbb {Q}_p^d$ , for $d = [K : \mathbb {Q}_p]$ . Under this interpretation, $GL_n(K)$ is interpreted as a subgroup of $GL_{nd}(\mathbb {Q}_p)$ , and therefore any affine group in (an elementary extension of) K is interpreted as an affine group in (an elementary extension of) $\mathbb {Q}_p$ . This shows that Theorem 5.12 extends from $\mathbb {Q}_p$ to its finite extensions, and then the other proofs carry through with minimal changes.

Theorem 5.13 has the following corollary:

Corollary 5.15. Let G be a definably amenable group defined in $\mathbb {Q}_p$ . There is a finite index definable subgroup $E \subseteq G$ and a finite normal subgroup $F \lhd E$ such that the quotient $E/F$ is isomorphic to an open subgroup of an algebraic group over $\mathbb {Q}_p$ .

Proof Like Corollary 4.3 in [13].