Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-28T04:15:13.101Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE UNCOUNTABILITY OF 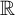${\mathbb R}$

Part of: General logic Proof theory and constructive mathematics Computability and recursion theory

Published online by Cambridge University Press:  07 April 2022

DAG NORMANN  and
SAM SANDERS
DAG NORMANN
Affiliation:
DEPARTMENT OF MATHEMATICS THE UNIVERSITY OF OSLO P.O. BOX 1053, BLINDERN N-0316OSLO, NORWAYE-mail:[email protected]
SAM SANDERS*
Affiliation:
DEPARTMENT OF PHILOSOPHY II RUHR-UNIVERSITÄT BOCHUM (RUB)BOCHUM, GERMANY
*
E-mail:[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Cantor’s first set theory paper (1874) establishes the uncountability 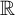of ${\mathbb R}$ . We study this most basic mathematical fact formulated in the language of higher-order arithmetic. In particular, we investigate the logical and computational properties of ${\mathsf {NIN}}$ (resp. ${\mathsf {NBI}}$ ), i.e., the third-order statement there is no injection resp. bijection from 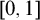 $[0,1]$ to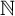 ${\mathbb N}$ . Working in Kohlenbach’s higher-order Reverse Mathematics, we show that ${\mathsf {NIN}}$ and ${\mathsf {NBI}}$ are hard to prove in terms of (conventional) comprehension axioms, while many basic theorems, like Arzelà’s convergence theorem for the Riemann integral (1885), are shown to imply ${\mathsf {NIN}}$ and/or ${\mathsf {NBI}}$ . Working in Kleene’s higher-order computability theory based on S1–S9, we show that the following fourth-order process based on ${\mathsf {NIN}}$ is similarly hard to compute: for a given 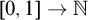$[0,1]\rightarrow {\mathbb N}$ -function, find reals in the unit interval that map to the same natural number.

Keywords

Uncountability of ℝReverse MathematicsKleene S1–S9higher-order computability theory

MSC classification

Primary: 03B30: Foundations of classical theories (including reverse mathematics)
Secondary: 03F35: Second- and higher-order arithmetic and fragments 03D55: Hierarchies 03D30: Other degrees and reducibilities
Type
Article
Information
The Journal of Symbolic Logic , Volume 87 , Issue 4 , December 2022 , pp. 1474 - 1521
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aharoni, R., Magidor, M., and Shore, R. A., On the strength of König’s duality theorem for infinite bipartite graphs . Journal of Combinatorial Theory, Series B , vol. 54 (1992), no. 2, pp. 257–290.CrossRefGoogle Scholar
Arzelà, C., Sulla integrazione per serie . Atti della Accademia Nazionale dei Lincei. Rendiconti Lincei. Matematica e Applicazioni , vol. 1 (1885), pp. 532–537.Google Scholar
Avigad, J. and Feferman, S., Gödel’s functional “Dialectica” interpretation , Handbook of Proof Theory (Sam Buss, editor), Studies in Logic and the Foundations of Mathematics, vol. 137, Elsevier, Amsterdam, 1998, pp. 337–405.CrossRefGoogle Scholar
Baire, R., Sur les fonctions de variables réelles . Annali di Matematica , vol. 3 (1899), no. 3, pp. 1–123.CrossRefGoogle Scholar
Baire, R., Leçons Sur les fonctions discontinues , Les Grands Classiques Gauthier-Villars, Éditions Jacques Gabay, Sceaux, 1995 (in French). Reprint of the 1905 original.Google Scholar
Barbu, V. and Precupanu, T., Convexity and Optimization in Banach Spaces , fourth ed., Springer Monographs in Mathematics, Springer, Dordrecht, 2012.CrossRefGoogle Scholar
Bauer, A., An injection from the Baire space to natural numbers . Mathematical Structures in Computer Science , vol. 25 (2015), no. 7, pp. 1484–1489.CrossRefGoogle Scholar
Beth, E. W., Semantic Entailment and Formal Derivability , Mededelingen der koninklijke Nederlandse Akademie van Wetenschappen, Afd. Letterkunde, Nieuwe Reeks, Deel 18, Vol. 13, N. V. Noord-Hollandsche Uitgevers Maatschappij, Elsevier, Amsterdam, 1955.Google Scholar
Bishop, E., Foundations of Constructive Analysis , McGraw-Hill, New York, 1967.Google Scholar
Blumberg, H., New properties of all real functions . Transactions of the American Mathematical Society , vol. 24 (1922), no. 2, pp. 113–128.CrossRefGoogle Scholar
du Bois-Reymond, P., Die allgemeine Functionentheorie I , Wissenschaftliche Buchgesellschaft, Darmstadt, 1968 (in German). Part I, reproduction of the 1882 original with afterword and selected bibliography by Detlef Laugwitz.Google Scholar
Borel, E., Leçons Sur la théorie Des Fonctions , Gauthier-Villars, Paris, 1898.Google Scholar
Bressoud, D. M., A Radical Approach to Lebesgue’s Theory of Integration , MAA Textbooks, Cambridge University Press, Cambridge, 2008.Google Scholar
Brown, D. K., Notions of compactness in weak subsystems of second order arithmetic , Reverse Mathematics 2001 (Stephen Simson, editor), Lecture Notes in Logic, vol. 21, Association for Symbolic Logic, La Jolla, 2005, pp. 47–66.Google Scholar
Brown, D. K., Giusto, M., and Simpson, S. G., Vitali’s theorem and WWKL . Archive for Mathematical Logic , vol. 41 (2002), no. 2, pp. 191–206.CrossRefGoogle Scholar
Buchholz, W., Feferman, S., Pohlers, W., and Sieg, W., Iterated Inductive Definitions and Subsystems of Analysis , Lecture Notes in Mathematics, vol. 897, Springer, New York, 1981.Google Scholar
Cantor, G., Ueber eine Eigenschaft des Inbegriffs aller reellen algebraischen Zahlen . Journal für die Reine und Angewandte Mathematik , vol. 77 (1874), pp. 258–262.Google Scholar
Cantor, G., Ein Beitrag zur Mannigfaltigkeitslehre . Journal für die reine und angewandte Mathematik , vol. 84 (1877), pp. 242–258.Google Scholar
Cantor, G., Ueber unendliche, lineare Punktmannichfaltigkeiten. Mathematische Annalen , vols. 17–23. Published in parts: 1879–1884.CrossRefGoogle Scholar
Cantor, G., Mitteilungen zur Lehre vom Transfiniten , Pfeffer, 1887.Google Scholar
Cantor, G., Gesammelte Abhandlungen Mathematischen und Philosophischen Inhalts , Springer, Berlin, 1980. Reprint of the 1932 original.Google Scholar
Carslaw, H. S., Term-by-term integration of infinite series . The Mathematical Gazette , vol. 13 (1927), pp. 437–441.CrossRefGoogle Scholar
Cohen, P., The independence of the continuum hypothesis . Proceedings of the National Academy of Sciences of the United States of America , vol. 50 (1963), pp. 1143–1148.CrossRefGoogle ScholarPubMed
Cohen, P., The independence of the continuum hypothesis. II . Proceedings of the National Academy of Sciences of the United States of America , vol. 51 (1964), pp. 105–110.CrossRefGoogle ScholarPubMed
Cousin, P., Sur les fonctions de $n$ variables complexes . Acta Mathematica , vol. 19 (1895), pp. 1–61.CrossRefGoogle Scholar
Dauben, J. W. and Cantor, G., editors, His Mathematics and Philosophy of the Infinite , Princeton University Press, Princeton, 1990.Google Scholar
Devlin, K. J., Constructibility , Perspectives in Mathematical Logic, Springer, New York, 1984.CrossRefGoogle Scholar
Diener, H., Variations on a theme by Ishihara . Mathematical Structures in Computer Science , vol. 25 (2015), no. 7, pp. 1569–1577.CrossRefGoogle Scholar
Diestel, J. and Swart, J., The Riesz theorem , Handbook of Measure Theory, vol. I (E. Pap, editor), North-Holland, Amsterdam, 2002, pp. 401–447.Google Scholar
Dini, U., Fondamenti per la Teorica Delle Funzioni di Variabili Reali , Nistri, Pisa, 1878.Google Scholar
Dzhafarov, D. D., Reverse Mathematics Zoo. http://rmzoo.uconn.edu/.Google Scholar
Ewald, W., editor, From Kant to Hilbert: A Source Book in the Foundations of Mathematics, vols. I and II , Oxford Science Publications, Oxford University Press, Oxford, 1996.Google Scholar
Feferman, S., How a little bit goes a long way: Predicative foundations of analysis, 2013, unpublished notes from 1977 to 1981 with updated introduction. Available at https://math.stanford.edu/feferman/papers/pfa(1).pdf.Google Scholar
Ferreirós, J., Labyrinth of Thought: A History of Set Theory and Its Role in Modern Mathematics , second ed., Birkhäuser, Basel, 2007.Google Scholar
Fréchet, M., Sur quelques points du Calcul Fonctionel . Rendiconti del Circolo Matematico di Palermo , vol. XXII (1906), pp. 1–72.Google Scholar
Friedman, H., Some systems of second order arithmetic and their use , Proceedings of the International Congress of Mathematicians (Vancouver, BC, 1974) , vol. 1 , 1975, pp. 235–242.Google Scholar
Friedman, H., Systems of second order arithmetic with restricted induction, I & II (abstracts), this Journal, vol. 41 (1976), pp. 557–559.Google Scholar
Gandy, R., General recursive functionals of finite type and hierarchies of functions . Annales scientifiques de l’Université de Clermont. Mathématiques , vol. 35 (1967), pp. 5–24.Google Scholar
Gödel, K., The consistency of the axiom of choice and of the generalized continuum-hypothesis . Proceedings of the National Academy of Science , vol. 24 (1938), no. 12, pp. 556–557.CrossRefGoogle ScholarPubMed
Gordon, R. A., A convergence theorem for the Riemann integral . Mathematics Magazine , vol. 73 (2000), no. 2, pp. 141–147.CrossRefGoogle Scholar
Gray, R., Georg Cantor and transcendental numbers . American Mathematical Monthly , vol. 101 (1994), no. 9, pp. 819–832.CrossRefGoogle Scholar
Hankel, H., Untersuchungen über die unendlich oft oscillirenden und unstetigen Functionen . Mathematische Annalen , vol. 20 (1882), no. 1, pp. 63–112 (in German).CrossRefGoogle Scholar
Harnack, A., Vereinfachung der Beweise in der Theorie der Fourier’schen Reihe . Mathematische Annalen , vol. 19 (1881), no. 2, pp. 235–279 (in German).CrossRefGoogle Scholar
Harnack, A., Ueber den Inhalt von Punktmengen . Mathematische Annalen , vol. 25 (1885), pp. 241–250.CrossRefGoogle Scholar
Hartley, J. P., The countably based functionals, this Journal, vol. 48 (1983), no. 2, pp. 458–474.Google Scholar
Hawkins, T., Lebesgue’s Theory of Integration: Its Origins and Development , second ed., AMS Chelsea, Providence, 2001.Google Scholar
Helly, E., Über lineare Funktionaloperationen . Sitzungsberichte der Mathematisch-Naturwissenschaftlichen Klasse der Kaiserlichen Akademie der Wissenschaften, Wien , vol. 121 (1912), pp. 265–297.Google Scholar
Hilbert, D., Über das Unendliche . Mathematische Annalen , vol. 95 (1926), no. 1, pp. 161–190 (in German).CrossRefGoogle Scholar
Hilbert, D., Mathematical problems . Bulletin of the American Mathematical Society , vol. 37 (2000), no. 4, pp. 407–436. Reprinted from Bulletin of the American Mathematical Society , vol. 8 (1902), pp. 437–479.CrossRefGoogle Scholar
Howard, P. and Rubin, J. E., Consequences of the Axiom of Choice , Mathematical Surveys and Monographs, vol. 59, American Mathematical Society, Providence, 1998.CrossRefGoogle Scholar
Hrbacek, K. and Jech, T., Introduction to Set Theory , third ed., Monographs and Textbooks in Pure and Applied Mathematics, vol. 220, Marcel Dekker, New York, 1999.Google Scholar
Hunter, J., Higher-Order Reverse Topology , ProQuest LLC, Ann Arbor, 2008, Ph.D. thesis, The University of Wisconsin, Madison.Google Scholar
Hunter, J. K. and Nachtergaele, B., Applied Analysis , World Scientific, River Edge, 2001.CrossRefGoogle Scholar
Katz, M. and Reimann, J., An Introduction to Ramsey Theory: Fast Functions, Infinity, and Metamathematics , Student Mathematical Library, vol. 87, American Mathematical Society, Providence; Mathematics Advanced Study Semesters, University Park, 2018.CrossRefGoogle Scholar
Kelley, J. L., General Topology , Graduate Texts in Mathematics, vol. 27, Springer, Berlin, 1975. Reprint of the 1955 edition.Google Scholar
Kestelman, H., Riemann integration of limit functions . American Mathematical Monthly , vol. 77 (1970), no. 2, pp. 182–187.CrossRefGoogle Scholar
Kihara, T., Marcone, A., and Pauly, A., Searching for an analogue of ${\mbox{ATR}}_0$ in the Weihrauch lattice, this Journal, vol. 85 (2020), pp. 1006–1043.Google Scholar
Kleene, S. C., Recursive functionals and quantifiers of finite types. I . Transactions of the American Mathematical Society , vol. 91 (1959), pp. 1–52.Google Scholar
Kleiner, I., Excursions in the History of Mathematics , Birkhäuser/Springer, Berlin, 2012.CrossRefGoogle Scholar
Kohlenbach, U., Foundational and mathematical uses of higher types , Reflections on the Foundations of Mathematics (Wilfied Sieg, Richard Sommer, and Carolyn Talcott, editors), Lecture Notes in Logic, vol. 15, Association for Symbolic Logic, Urbana, 2002, pp. 92–116.Google Scholar
Kohlenbach, U., Higher order reverse mathematics , Reverse Mathematics 2001 (Stephen Simson, editor), Lecture Notes in Logic, vol. 21, Association for Symbolic Logic, La Jolla, 2005, pp. 281–295.Google Scholar
Kohlenbach, U., Applied Proof Theory: Proof Interpretations and Their Use in Mathematics , Springer Monographs in Mathematics, Springer, Berlin, 2008.Google Scholar
Kolmogorov, A. N., Foundations of the Theory of Probability , Chelsea, New York, 1950.Google Scholar
König, D., Über eine Schlussweise aus dem Endlichen ins Unendliche . Acta Litterarum ac Scientarum (Sectio Scientiarum Mathematicarum) Szeged , vol. 3 (1927), pp. 121–130.Google Scholar
Kreuzer, A. P., Bounded variation and the strength of Helly’s selection theorem , Logical Methods in Computer Science , vol. 10 (2014), no. 4, p. 4:16, 15.CrossRefGoogle Scholar
Kreuzer, A. P., Measure theory and higher order arithmetic . Proceedings of the American Mathematical Society , vol. 143 (2015), no. 12, pp. 5411–5425.CrossRefGoogle Scholar
Kunen, K., Set Theory , Studies in Logic, vol. 34, College Publications, London, 2011.Google Scholar
Longley, J. and Normann, D., Higher-Order Computability , Theory and Applications of Computability, Springer, Berlin, 2015.CrossRefGoogle Scholar
Luckhardt, H., The real elements in a consistency proof for simple type theory I , ${\vDash}$ ISILC Proof Theory Symposion (Proceedings of the International Summer Institute and Logic Colloquium, Kiel, 1974) (Justus Diller and Gert H. Müller, editors), Lecture Notes in Mathematics, vol. 500, Springer, Berlin, 1975, pp. 233–256.Google Scholar
Luxemburg, W. A. J., Arzelà’s dominated convergence theorem for the Riemann integral . American Mathematical Monthly , vol. 78 (1971), pp. 970–979.Google Scholar
Moore, E. H., On a form of general analysis with application to linear differential and integral equations . Atti IV Cong. Inter. Mat. (Roma, 1908) , vol. 2 (1909), pp. 98–114.Google Scholar
Moore, E. H., Introduction to a Form of General Analysis , Yale University Press, New Haven, 1910.CrossRefGoogle Scholar
Moore, E. H., Definition of limit in general integral analysis . Proceedings of the National Academy of Sciences of the United States of America , vol. 1 (1915), no. 12, pp. 628–632.CrossRefGoogle ScholarPubMed
Moore, E. H., On power series in general analysis , Festschrift David Hilbert zu seinem Sechzigsten Geburtstag am 23. Januar 1922 , Springer, 1922, pp. 355–364.CrossRefGoogle Scholar
Moore, E. H., On power series in general analysis . Mathematische Annalen , vol. 86 (1922), nos. 1–2, pp. 30–39.CrossRefGoogle Scholar
Moore, E. H. and Smith, H., A general theory of limits . American Journal of Mathematics , vol. 44 (1922), pp. 102–121.CrossRefGoogle Scholar
Muldowney, P., A General Theory of Integration in Function Spaces, Including Wiener and Feynman Integration , Pitman Research Notes in Mathematics Series, vol. 153, Longman Scientific & Technical, Harlow; Wiley, New York, 1987.Google Scholar
Mummert, C., On the Reverse Mathematics of General Topology , ProQuest LLC, Ann Arbor, 2005, Ph.D. thesis, The Pennsylvania State University.Google Scholar
Mummert, C., Reverse mathematics of MF spaces . Journal of Mathematical Logic , vol. 6 (2006), no. 2, pp. 203–232.CrossRefGoogle Scholar
Mummert, C. and Simpson, S. G., Reverse mathematics and  ${\Pi}_2^1$  comprehension . Bulletin of Symbolic Logic , vol. 11 (2005), no. 4, pp. 526–533.CrossRefGoogle Scholar
Nies, A., Triplett, M. A., and Yokoyama, K., The reverse mathematics of theorems of Jordan and Lebesgue, this Journal, vol. 86 (2021), pp. 1657–1675.Google Scholar
Normann, D., Functionals of type 3 as realisers of classical theorems in analysis , Proceedings of CiE18 (Florin Manea, Russell G. Miller, and Dirk Nowotka, editors), Lecture Notes in Computer Science, vol. 10936, Springer, New York, 2018, pp. 318–327.Google Scholar
Normann, D., Computability and non-monotone induction, preprint, 2020, arXiv:2006.03389, p. 41.Google Scholar
Normann, D. and Sanders, S., Nonstandard analysis, computability theory, and their connections, this Journal, vol. 84 (2019), no. 4, pp. 1422–1465.Google Scholar
Normann, D. and Sanders, S., The strength of compactness in computability theory and nonstandard analysis . Annals of Pure and Applied Logic , vol. 170 (2019), no. 11, 102710.CrossRefGoogle Scholar
Normann, D. and Sanders, S., On the mathematical and foundational significance of the uncountable . Journal of Mathematical Logic , vol. 19 (2019), 1950001.CrossRefGoogle Scholar
Normann, D. and Sanders, S., Open sets in reverse mathematics and computability theory . Journal of Logic and Computability , vol. 30 (2020), no. 8, p. 40.Google Scholar
Normann, D. and Sanders, S., Pincherle’s theorem in reverse mathematics and computability theory . Annals of Pure and Applied Logic , vol. 171 (2020), no. 5, 102788, p. 41.CrossRefGoogle Scholar
Normann, D. and Sanders, S., The axiom of choice in computability theory and reverse mathematics with a cameo for the continuum hypothesis . Journal of Logic and Computation , vol. 31 (2021), pp. 297–325.CrossRefGoogle Scholar
Normann, D. and Sanders, S., On robust theorems due to Bolzano, Weierstrass, and Cantor in reverse mathematics, preprint, 2021, arXiv:2102.04787, p. 30.Google Scholar
Normann, D. and Sanders, S., On the logical and computational properties of the Vitali covering theorem, preprint, 2022, arXiv:1902.02756.Google Scholar
Normann, D. and Sanders, S., Betwixt Turing and Kleene , Logical Foundations of Computer Science (Artemov, S. and Nerode, A., editors), Lecture Notes in Computer Science, vol. 13137, Springer, Cham, 2022, pp. 236–252.CrossRefGoogle Scholar
Normann, D. and Sanders, S., On the computational properties of basic mathematical notions, preprint, 2022, arxiv:2203.05250, p. 43.Google Scholar
Oliva, P. and Powell, T., Bar recursion over finite partial functions . Annals of Pure and Applied Logic , vol. 168 (2017), no. 5, pp. 887–921.CrossRefGoogle Scholar
Rathjen, M., The Art of Ordinal Analysis , International Congress of Mathematicians, vol. II, European Mathematical Society, Zürich, 2006.Google Scholar
Royden, H. L. and Fitzpatrick, P. M., Real Analysis , fourth ed., Pearson, New York, 2010.Google Scholar
Sakamoto, N. and Yamazaki, T., Uniform versions of some axioms of second order arithmetic . MLQ , vol. 50 (2004), no. 6, pp. 587–593.CrossRefGoogle Scholar
Sanders, S., Plato and the foundations of mathematics, preprint, 2020, arxiv:1908.05676.Google Scholar
Sanders, S., Lifting recursive counterexamples to higher-order arithmetic , Logical Foundations of Computer Science. LFCS 2020 (Artemov, S. and Nerode, A., editors), Lecture Notes in Computer Science, vol. 11972, Springer, Cham, 2020, pp. 249–267.Google Scholar
Sanders, S., Reverse mathematics of topology: Dimension, paracompactness, and splittings . Notre Dame J. for Formal Logic , vol. 61 (2020), no. 4, pp. 537–559.Google Scholar
Sanders, S., Lifting countable to uncountable mathematics, Information and Computation , 104762 (2021). https://doi.org/10.1016/j.ic.2021.104762.CrossRefGoogle Scholar
Sanders, S., Representations and the foundations of mathematics, Notre Dame Journal of Formal Logic , vol. 63 (2022), no. 1, pp. 1–28.Google Scholar
Sanders, S., Reverse mathematics of the uncountability of $\mathbb{R}$ , preprint, 2022, arXiv:2203.05292, p. 12.Google Scholar
Sanders, S. and Yokoyama, K., The Dirac delta function in two settings of reverse mathematics . Archive for Mathematical Logic , vol. 51 (2012), no. 1, pp. 99–121.CrossRefGoogle Scholar
Shafer, P., The strength of compactness for countable complete linear orders . Computability , vol. 9 (2020), no. 1, pp. 25–36.CrossRefGoogle Scholar
Sierpiński, W., Sur un problème de la théorie des relations . Annali della Scuola Normale Superiore di Pisa—Classe di Scienze, Série 2 , vol. 2 (1933), no. 3, pp. 285–287 (in French).Google Scholar
Simpson, S. G., editor, Reverse Mathematics 2001 , Lecture Notes in Logic, vol. 21, Association for Symbolic Logic, La Jolla, 2005.Google Scholar
Simpson, S. G., Subsystems of Second Order Arithmetic , second ed., Perspectives in Logic, Cambridge University Press, Cambridge, 2009.CrossRefGoogle Scholar
Simpson, S. G., The Gödel hierarchy and reverse mathematics . Kurt Gödel. Essays for His Centennial (Solomon Feferman, Charles Parsons, and Stephen G. Simpson, editors), Association for Symbolic Logic, Providence, 2010, pp. 109–127.CrossRefGoogle Scholar
Smith, H. J. S., On the integration of discontinuous functions , Proceedings of the London Mathematical Society , vol. 6 (1874/75), pp. 140–153.CrossRefGoogle Scholar
Sohrab, H. H., Basic Real Analysis , second ed., Birkhäuser/Springer, New York, 2014.Google Scholar
Stillwell, J., Roads to Infinity: The Mathematics of Truth and Proof , A K Peters, Natick, 2010.CrossRefGoogle Scholar
Stillwell, J., The Real Numbers: An Introduction to Set Theory and Analysis , Undergraduate Texts in Mathematics, Springer, Cham, 2013.CrossRefGoogle Scholar
Stillwell, J., Reverse Mathematics: Proofs from the Inside Out , Princeton University Press, Princeton, 2018.Google Scholar
Swartz, C., Introduction to Gauge Integrals , World Scientific, Singapore, 2001.CrossRefGoogle Scholar
Tao, T., Structure and Randomness: Pages from Year One of a Mathematical Blog , American Mathematical Society, Providence, 2008.CrossRefGoogle Scholar
Tao, T., An Epsilon of Room, I: Real Analysis , Graduate Studies in Mathematics, vol. 117, American Mathematical Society, Providence, 2010.Google Scholar
Tao, T., An Introduction to Measure Theory , Graduate Studies in Mathematics, vol. 126, American Mathematical Society, Providence, 2011.Google Scholar
Thomson, B., Monotone convergence theorem for the Riemann integral . American Mathematical Monthly , vol. 117 (2010), no. 6, pp. 547–550.CrossRefGoogle Scholar
Troelstra, A. S., Metamathematical Investigation of Intuitionistic Arithmetic and Analysis , Lecture Notes in Mathematics, vol. 344, Springer, Berlin, 1973.CrossRefGoogle Scholar
Troelstra, A. S. and van Dalen, D., Constructivism in Mathematics , vol. I , Studies in Logic and the Foundations of Mathematics, 121, Elsevier, Amsterdam, 1988.Google Scholar
Troelstra, A. S. and van Dalen, D., Constructivism in Mathematics , vol. II , Studies in Logic and the Foundations of Mathematics, 123, Elsevier, Amsterdam, 1988.Google Scholar
Tukey, J. W., Convergence and Uniformity in Topology , Annals of Mathematics Studies, vol. 2, Princeton University Press, Princeton, 1940.Google Scholar
Turing, A., On computable numbers, with an application to the Entscheidungsproblem . Proceedings of the London Mathematical Society , vol. 42 (1936), pp. 230–265.Google Scholar
Vitali, G., Sui gruppi di punti e sulle funzioni di variabili reali . Atti della Accademia delle Scienze di Torino , vol. XLIII (1907), pp. 229–247.Google Scholar
Weaver, G., König’s infinity lemma and Beth’s tree theorem . History and Philosophy of Logic , vol. 38 (2017), no. 1, pp. 48–56.CrossRefGoogle Scholar
Wikipedia Contributors, Cantor’s First Set Theory Article, Wikipedia, the Free Encyclopedia, 2020. Available at https://en.wikipedia.org/wiki/Cantor%27s_first_set_theory_article.Google Scholar
Yokoyama, K., Standard and Non-Standard Analysis in Second Order Arithmetic , Tohoku Mathematical Publications, vol. 34, Tohoku University, Sendai, 2009, Ph.D. thesis, Tohoku University, 2007.Google Scholar
Young, W. H., On non-uniform convergence and term-by-term integration of series . Proceedings of the London Mathematical Society. Second Series , vol. 1 (1904), pp. 89–102.CrossRefGoogle Scholar