Hostname: page-component-745bb68f8f-hvd4g Total loading time: 0 Render date: 2025-01-14T02:44:40.377Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Optimality of Conservation Results for Local Reflection in Arithmetic

Published online by Cambridge University Press:  12 March 2014

A. Cordón-Franco ,
A. Fernández-Margarit  and
F. F. Lara-Martín
A. Cordón-Franco
Affiliation:
Departamento Ciencias de la Computación e Inteligencia Artificial, Facultad de Matemáticas., Universidad de Sevilla, C/Tarfia, S/N, 41012 Sevilla, Spain, E-mail: [email protected]
A. Fernández-Margarit
Affiliation:
Departamento Ciencias de la Computación e Inteligencia Artificial, Facultad de Matemáticas., Universidad de Sevilla, C/Tarfia, S/N, 41012 Sevilla, Spain
F. F. Lara-Martín
Affiliation:
Departamento Ciencias de la Computación e Inteligencia Artificial, Facultad de Matemáticas., Universidad de Sevilla, C/Tarfia, S/N, 41012 Sevilla, Spain, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let T be a recursively enumerable theory extending Elementary Arithmetic EA. L. D. Beklemishev proved that the Σ2 local reflection principle for T, 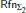(T), is conservative over the Σ1 local reflection principle, 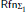(T), with respect to boolean combinations of Σ1-sentences; and asked whether this result is best possible. In this work we answer Beklemishev's question by showing that Π2-sentences are not conserved for T = EA + “f is total,” where f is any nondecreasing computable function with elementary graph. We also discuss how this result generalizes to n > 0 and obtain as an application that for n > 0, 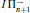is conservative over IΣn with respect to Πn+2-sentences.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 78 , Issue 4 , December 2013 , pp. 1025 - 1035
Copyright
Copyright © Association for Symbolic Logic 2013

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Avigad, J., Saturated models of universal theories, Annals of Pure and Applied Logic, vol. 118 (2002), pp. 219–234.CrossRefGoogle Scholar
[2] Beklemishev, L. D., Induction rules, reflection principles, and provably recursive functions, Annals of Pure and Applied Logic, vol. 85 (1997), pp. 193–242.Google Scholar
[3] Beklemishev, L. D., Notes on local reflection principles, Theoria, vol. 63 (1997), pp. 139–146.Google Scholar
[4] Beklemishev, L. D., Parameter free induction and provably total computable functions, Theoretical Computer Science, vol. 224 (1999), pp. 13–33.CrossRefGoogle Scholar
[5] Beklemishev, L. D., Proof-theoretic analysis by iterated reflection, Archive for Mathematical Logic, vol. 42 (2005), pp. 515–552.Google Scholar
[6] Beklemishev, L. D., Reflection principles and provability algebras in formal arithmetic, Russian Mathematical Surveys, vol. 60 (2005), pp. 197–268.Google Scholar
[7] Cordón-Franco, A., Fernández-Margarit, A., and Lara-Martín, F. F., On conservation results for parameter–free πn–induction, Studies in weak arithmetics (Cégielski, P., editor), CSLI Lecture Notes, vol. 196, The University of Chicago Press, 2010, pp. 49–97.Google Scholar
[8] Cordón-Franco, A., Fernández-Margarit, A., and Lara-Martín, F. F., A note on parameter free π1-induction and restricted exponentiation, Mathematical Logic Quarterly, vol. 57 (2011), pp. 444–455.Google Scholar
[9] Goryachev, S. V., On the interpretability of some extensions of arithmetic, Rossiĭskaya Akademiya Nauk. Matematicheskie Zametki, vol. 40 (1986), pp. 561–571.Google Scholar
[10] Hájek, P. and Pudlák, P., Metamathematics of first–order arithmetic, Perpectivesin Mathematical Logic, Springer–Verlag, 1993.Google Scholar
[11] Kaye, R., Models of Peano Arithmetic, Oxford Logic Guides, vol. 15, Oxford University Press, 1991.Google Scholar
[12] Kaye, R., Paris, J., and Dimitracopoulos, C., On parameter free induction schemas, this Journal, vol. 53 (1988), pp. 1082–1097.Google Scholar
[13] Kreisel, H. and Lévy, A., Reflection principles and their use for establishing the complexity of axiomatic systems, Zeitschrift für mathematische Logik und Grundlagen der Mathematik, vol. 14 (1968), pp. 97–142.Google Scholar
[14] Leivant, D., The optimality of induction as an axiomatization of arithmetic, this Journal, vol. 48 (1983), pp. 182–184.Google Scholar
[15] Ono, H., Reflection principles in fragments of peano arithmetic, Zeitschrift für mathematische Logik und Grundlagen der Mathematik, vol. 33 (1987), pp. 317–333.Google Scholar
[16] Paris, J. and Kirby, L., Σn-collection schemas in arithmetic, Logic colloquium 77 (Macintyre, A., Pacholski, L., and Paris, J., editors), North-Holland, 1978, pp. 285–296.Google Scholar
[17] Zambella, D., Notes on polynomial bounded arithmetic, this Journal, vol. 61 (1996), pp. 942–966.Google Scholar