Article contents
On the number of nonisomorphic models of an infinitary theory which has the infinitary order property. Part A
Published online by Cambridge University Press: 12 March 2014
Abstract
Let κ and λ be infinite cardinals such that λ ≤ λ (we have new information for the case when κ ≤ λ). Let T be a theory in Lκ
+,
ω
of cardinality at most κ, let 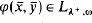 . Now define
. Now define
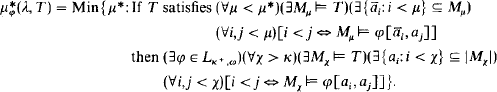
Our main concept in this paper is 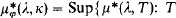 is a theory in Lκ
+,
ω
of cardinality κ at most, and φ(x, y) ϵ Lκ
+,
ω
}. This concept is interesting because of
is a theory in Lκ
+,
ω
of cardinality κ at most, and φ(x, y) ϵ Lκ
+,
ω
}. This concept is interesting because of
Theorem 1. Let T ⊆ Lκ +, ω of cardinality ≤ κ, and
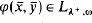 . If
. If
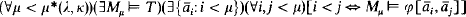
then (∀χ > κ)I(χ, T) = 2 χ (where I(χ, T) stands for the number of isomorphism types of models of T of cardinality χ).
Many years ago the second author proved that 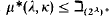 . Here we continue that work by proving
. Here we continue that work by proving
Theorem 2. 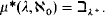 .
.
Theorem 3. For every
κ ≤ λ
we have
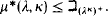 .
.
For some κ or λ we have better bounds than in Theorem 3, and this is proved via a new two cardinal theorem.
Theorem 4. For every T ⊆ Lκ +, ω, and any set of formulas
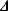 ⊆ Lκ +, ω such that
⊆ Lκ +, ω such that
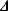 T ⊇ Lκ +, ω, if T is (
T ⊇ Lκ +, ω, if T is (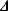 , μ)-unstable for μ satisfying
μμ*(λ,κ) = μ then T is
, μ)-unstable for μ satisfying
μμ*(λ,κ) = μ then T is
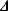 -unstable (i.e. for every χ ≥ λ, T is (
-unstable (i.e. for every χ ≥ λ, T is (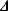 , χ)-unstable). Moreover, T is Lκ +, ω-unstable.
, χ)-unstable). Moreover, T is Lκ +, ω-unstable.
In the second part of the paper, we show that always in the applications it is possible to replace the function I(χ, T) by the function IE(χ, T), and we give an application of the theorems to Boolean powers.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1986
Footnotes
We would like to thank the United States-Israel Binational Science Foundation for partially supporting this research. We are grateful to the referee for a very long and detailed referee report. The first author received support from Harvey Friedman, whom he thanks.
References
REFERENCES
- 5
- Cited by


