Article contents
On the notational independence of various hierarchies of degrees of unsolvability1
Published online by Cambridge University Press: 12 March 2014
Extract
From the work of Kleene, Post and Davis it is well-known that the arithmetic sets can be characterized as those sets recursive in ∅(n) for some natural number n, where ∅(0) = ∅ and 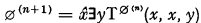 . Actually the arithmetic sets which can be expressed in prenex form with n alternating quantifiers (applied to recursive predicates) are recursive in ∅(n). Hence, starting with ∅, the “jump operation”, which takes a set A into the set
. Actually the arithmetic sets which can be expressed in prenex form with n alternating quantifiers (applied to recursive predicates) are recursive in ∅(n). Hence, starting with ∅, the “jump operation”, which takes a set A into the set 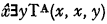 , serves to increase the “complexity” of sets in a uniform way.
, serves to increase the “complexity” of sets in a uniform way.
As far as extending the ω-sequence of degrees of unsolvability (i.e. the degrees represented by the ∅(n)) into the 2nd number class, there is an immediate problem. One knows from Spector [17], corollary 2, p. 585, that there is no l.u.b. for the ω-sequence. So, at ω one must pick a degree in some other “natural” way. Unfortunately, what has seemed “natural” to some mathematicians has not seemed natural to others. Kleene and Davis (cf. [10] and [3] respectively) extended this arithmetic hierarchy of degrees of unsolvability by making use of natural number notations for a certain segment of ordinals of the 1st and 2nd number classes, the “constructive” ordinals. Using the Church-Kleene system S3, one can “sum up” previously obtained sets at the limit notations in a way that is certainly natural from a notational point of view.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1965
Footnotes
Added September 23, 1964. Enderton's work has now appeared: Hierarchies in recursive function theory, Transactions of the American Mathematical Society, Vol. 111 (1964), pp. 457-471.
References
BIBLIOGRAPHY
- 1
- Cited by


