No CrossRef data available.
Published online by Cambridge University Press: 12 March 2014
Let A and B be subsets of the reals. Say that A
K
≥ B, if there is a real a such that the relation “x ∈ B” is uniformly ⊿1 (a, A) in 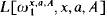 . This reducibility induces an equivalence relation ≡
K
on the sets of reals; the ≡
K
-equivalence class of a set is called its Kleene degree. Let
. This reducibility induces an equivalence relation ≡
K
on the sets of reals; the ≡
K
-equivalence class of a set is called its Kleene degree. Let 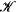 be the structure that consists of the Kleene degrees and the induced partial order
be the structure that consists of the Kleene degrees and the induced partial order
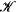 ≥. A substructure of
≥. A substructure of 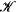 that is of interest is
that is of interest is 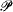 , the Kleene degrees of the
, the Kleene degrees of the 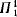 sets of reals. If sharps exist, then there is not much to
sets of reals. If sharps exist, then there is not much to 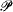 , as Steel [9] has shown that the existence of sharps implies that
, as Steel [9] has shown that the existence of sharps implies that 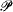 has only two elements: the degree of the empty set and the degree of the complete
has only two elements: the degree of the empty set and the degree of the complete 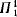 set. Legrand [4] used the hypothesis that there is a real whose sharp does not exist to show that there are incomparable elements in
set. Legrand [4] used the hypothesis that there is a real whose sharp does not exist to show that there are incomparable elements in 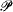 ; in the context of V = L, Hrbáček has shown that
; in the context of V = L, Hrbáček has shown that 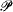 is dense and has no minimal pairs. The Hrbáček results led Simpson [6] to make the following conjecture: if V = L, then
is dense and has no minimal pairs. The Hrbáček results led Simpson [6] to make the following conjecture: if V = L, then 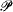 forms a universal homogeneous upper semilattice with 0 and 1. Simpson's conjecture is shown to be false by showing that if V = L, then Gödel's maximal thin
forms a universal homogeneous upper semilattice with 0 and 1. Simpson's conjecture is shown to be false by showing that if V = L, then Gödel's maximal thin 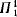 set is the infimum of two strictly larger elements of
set is the infimum of two strictly larger elements of 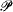 .
.
The second main result deals with the notion of jump in 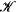 . Let A′ be the complete Kleene enumerable set relative to A. Say that A is low-n if A
(n) has the same degree as ⊘(n), and A is high-n if A(n)
has the same degree as ⊘(n+1). Simpson and Weitkamp [7] have shown that there is a high (high-1) incomplete
. Let A′ be the complete Kleene enumerable set relative to A. Say that A is low-n if A
(n) has the same degree as ⊘(n), and A is high-n if A(n)
has the same degree as ⊘(n+1). Simpson and Weitkamp [7] have shown that there is a high (high-1) incomplete 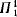 set in L. They have also shown that various other
set in L. They have also shown that various other 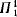 sets are neither high nor low in L. Legrand [5] extended their results by showing that, if there is a real x such that x#
does not exist, then there is an element of
sets are neither high nor low in L. Legrand [5] extended their results by showing that, if there is a real x such that x#
does not exist, then there is an element of 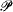 that, for all n, is neither low-n nor high-n. In §2, ZFC is used to show that, for all n, if A is
that, for all n, is neither low-n nor high-n. In §2, ZFC is used to show that, for all n, if A is 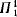 and low-n then A is Borel. The proof uses a strengthened version of Jensen's theorem on sequences of admissible ordinals that appears in [7, Simpson-Weitkamp].
and low-n then A is Borel. The proof uses a strengthened version of Jensen's theorem on sequences of admissible ordinals that appears in [7, Simpson-Weitkamp].