Article contents
On the compactness of ℵ1 and ℵ2
Published online by Cambridge University Press: 12 March 2014
Extract
In recent years, the Axiom of Determinateness (AD) has yielded numerous results concerning the size and properties of the first ω-many uncountable cardinals. Briefly, these results began with Solovay's discovery that ℵ1 and ℵ2 are measurable [8], [3], continued with theorems of Solovay, Martin, and Kunen concerning infinite-exponent partition relations [6], [3], Martin's proof that ℵn has confinality ℵ2 for 1 < n < ω, and very recently, Kleinberg's proof that the ℵn are Jonsson cardinals [4].
This paper was inspired by a very recent result of Martin from AD that ℵ1 is ℵ2-super compact. It was known for some time that AD implies ℵ1 is α-strongly compact for all ℵ < θ (where θ is the least cardinal onto which 2ω cannot be mapped, quite a large cardinal under AD), and that ADR implies that ℵ1, is α-super compact for all α < θ. A key open question had been whether or not ℵ1 is super compact under AD alone.
This paper comments on the method of Martin in several different ways. In §2, we will prove that ℵ1 is ℵ2-super compact, and then generalize the method to show that ℵ2 is ℵ3-strongly compact. In addition, we will demonstrate a limitation in the method by showing that the possible measures obtained on 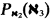 are not normal, and that the method cannot be extended to show that ℵ2 is ℵ4-strongly compact.
are not normal, and that the method cannot be extended to show that ℵ2 is ℵ4-strongly compact.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1978
References
REFERENCES
- 9
- Cited by


