Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-29T12:12:07.298Z Has data issue: false hasContentIssue false
  • English
  • Français

On the category of models of a complete theory

Published online by Cambridge University Press:  12 March 2014

Daniel Lascar
Daniel Lascar*
Affiliation:
Centre National De La Recherche Scientifique, Paris, France Mcgill University, Montreal, Quebec, Canada
Get access Rights & Permissions [Opens in a new window]

Extract

Let T be a countable complete theory and C(T) the category whose objects are the models of T and morphisms are the elementary maps. The main object of this paper will be the study of C(T). The idea that a better understanding of the category may give us model theoretic information about T is quite natural: The (semi) group of automorphisms (endomorphisms) of a given structure is often a powerful tool for studying this structure. But certainly, one of the very first questions to be answered is: “to what extent does this category C(T) determine T?”

There is some obvious limitation: for example let T0 be the theory of infinite sets (in a language containing only =) and T1 the theory, in the language ( =, U(ν0),f(ν0)) stating that:

(1) U is infinite.

(2)f is a bijective map from U onto its complement.

It is quite easy to see that C(T0) is equivalent to C(T1). But, in this case, T0 andT1 can be “interpreted” each in the other. To make this notion of interpretation precise, we shall associate with each theory T a category, loosely denoted by T, defined as follows:

(1) The objects are the formulas 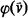in the given language.

(2) The morphisms from 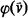into 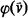are the formulas 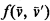such that

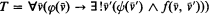
(i.e. f defines a map from ϕ into ϕ; two morphisms defining the same map in all models of T should be identified).

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 47 , Issue 2 , June 1982 , pp. 249 - 266
Copyright
Copyright © Association for Symbolic Logic 1982

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[LP]Lascar, D. and Poizat, B., An introduction to forking, this Journal, vol. 44 (1979), pp. 330–350.Google Scholar
[M1]Makkai, M., Full continuous embeddings of toposes (to appear).Google Scholar
[M2]Makkai, M., The topos of types (to appear).Google Scholar
[MR]Makkai, M. and Reyes, G., First order categorical logic, Lecture Notes in Mathematics, vol. 611, Springer-Verlag, Berlin and New York.Google Scholar
[S]Shelah, S., Classification theory and the number of non-isomorphic models, Studies in logic, North-Holland, Amsterdam, 1978.Google Scholar