Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-12-03T19:19:50.426Z Has data issue: false hasContentIssue false
  • English
  • Français

On the axioms of order and succession1

Published online by Cambridge University Press:  12 March 2014

Kurt Bing
Kurt Bing*
Affiliation:
Rensselaer Polytechnic Institute
Get access Rights & Permissions [Opens in a new window]

Extract

Hasenjaeger [2] has answered a question raised by Hilbert and Bernays [4] p. 279, by showing that the axiom

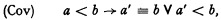
which, within lower predicate calculus, is independent of the remaining axioms of the system (B) p. 273, is no longer independent if the axiom 0 ≡ 0 of (B) is replaced by a ≡ a. The axioms from which (Cov) can be proved form the following system (B1) (obtained from (B), of course, by dropping (Cov) and replacing 0 ≡ 0 by a ≡ a):

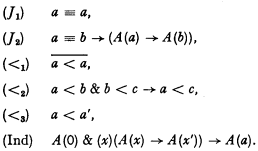
In what follows we consider (B1) and also the systems (B′) and (B′1) which are obtained from (B) and (B1) respectively by dropping the induction axiom and which clarify the role of the induction axiom.

1. (B1) is equivalent to (B). For (B) can be obtained from (B1) by Hasenjaeger's result. On the other hand, by pp. 263 and 261, the axioms (<1) and (J1) of (B1) can be proved from the axioms (<3) and

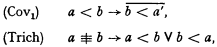
which belong to the system (A) p. 263. Therefore (B1) can be obtained from (A) and the induction axiom, and hence from (B).

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 22 , Issue 2 , June 1957 , pp. 141 - 144
Copyright
Copyright © Association for Symbolic Logic 1957

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

The results of this paper were obtained while the author was working on a research project sponsored by the International Business Machine Corporation, New York.

References

REFERENCES

[1]Church, Alonzo, Introduction to mathematical logic, vol. 1, Princeton (Princeton University Press), 1956.Google Scholar
[2]Hasenjaeger, G., Ein Beitrag zur Ordnungstheorie, Archiv für Mathematisehe Logik and Grundlagenforschung, vol. 1 (1950), pp. 30–31.CrossRefGoogle Scholar
[3]Hasenjaeger, G., Über ω-Unvollständigkeit in der Peano-Arithmetik, this Journal, vol. 17 (1952), pp. 81–97.Google Scholar
[4]Hilbert, D. and Bernays, P., Grundlagen der Mathematik, vol. 1, Berlin (Springer), 1934.Google Scholar