Article contents
On spectra, and the negative solution of the decision problem for identities having a finite nontrivial model1
Published online by Cambridge University Press: 12 March 2014
Extract
An algorithm has been described by S. Burris [3] which decides if a finite set of identities, whose function symbols are of rank at most 1, has a finite, nontrivial model. (By “nontrivial” it is meant that the universe of the model has at least two elements.) As a consequence of some results announced in the abstracts [2] and [8], it is clear that if the restriction on the ranks of function symbols is relaxed somewhat, then this finite model problem is no longer solvable by an algorithm, or at least not by a “recursive algorithm” as the term is used today.
In this paper we prove a sharp form of this negative result; showing, by the way, that Burris' result is in a sense the best possible result in the positive direction. Our main result is that in a first order language whose only function or relation symbol is a 2-place function symbol 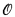 (the language of groupoids), the set of identities
(the language of groupoids), the set of identities 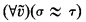 that have no nontrivial model, is recursively inseparable from the set of identities
that have no nontrivial model, is recursively inseparable from the set of identities 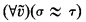 such that the sentence
such that the sentence 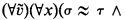
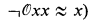 has a finite model. As a corollary, we have that each of the following problems, restricted to sentences defined in the language of groupoids, is algorithmically unsolvable: (1) to decide if an identity has a finite nontrivial model; (2) to decide if an identity has a nontrivial model; (3) to decide if a universal sentence has a finite model; (4) to decide if a universal sentence has a model. We note that the undecidability of (2) was proved earlier by McNulty [13, Theorem 3.6(i)], improving results obtained by Murskiǐ [14] and by Perkins [17]. The other parts of the corollary seem to be new.
has a finite model. As a corollary, we have that each of the following problems, restricted to sentences defined in the language of groupoids, is algorithmically unsolvable: (1) to decide if an identity has a finite nontrivial model; (2) to decide if an identity has a nontrivial model; (3) to decide if a universal sentence has a finite model; (4) to decide if a universal sentence has a model. We note that the undecidability of (2) was proved earlier by McNulty [13, Theorem 3.6(i)], improving results obtained by Murskiǐ [14] and by Perkins [17]. The other parts of the corollary seem to be new.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1975
Footnotes
The main result of this paper was announced in [12].
References
REFERENCES
- 44
- Cited by


