Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Monk, J. Donald
2010.
Special subalgebras of Boolean algebras.
MLQ,
Vol. 56,
Issue. 2,
p.
148.
Monk, J. Donald
2012.
Remarks on continuum cardinals on Boolean algebras.
Mathematical Logic Quarterly,
Vol. 58,
Issue. 3,
p.
159.
Monk, J. Donald
2018.
A large list of small cardinal characteristics of Boolean algebras.
Mathematical Logic Quarterly,
Vol. 64,
Issue. 4-5,
p.
336.


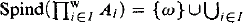 Spind(
Spind(