Article contents
ON SEQUENCES OF HOMOMORPHISMS INTO MEASURE ALGEBRAS AND THE EFIMOV PROBLEM
Published online by Cambridge University Press: 13 September 2021
Abstract
For given Boolean algebras
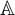 $\mathbb {A}$
and
$\mathbb {A}$
and
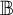 $\mathbb {B}$
we endow the space
$\mathbb {B}$
we endow the space
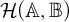 $\mathcal {H}(\mathbb {A},\mathbb {B})$
of all Boolean homomorphisms from
$\mathcal {H}(\mathbb {A},\mathbb {B})$
of all Boolean homomorphisms from
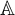 $\mathbb {A}$
to
$\mathbb {A}$
to
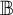 $\mathbb {B}$
with various topologies and study convergence properties of sequences in
$\mathbb {B}$
with various topologies and study convergence properties of sequences in
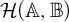 $\mathcal {H}(\mathbb {A},\mathbb {B})$
. We are in particular interested in the situation when
$\mathcal {H}(\mathbb {A},\mathbb {B})$
. We are in particular interested in the situation when
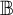 $\mathbb {B}$
is a measure algebra as in this case we obtain a natural tool for studying topological convergence properties of sequences of ultrafilters on
$\mathbb {B}$
is a measure algebra as in this case we obtain a natural tool for studying topological convergence properties of sequences of ultrafilters on
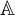 $\mathbb {A}$
in random extensions of the set-theoretical universe. This appears to have strong connections with Dow and Fremlin’s result stating that there are Efimov spaces in the random model. We also investigate relations between topologies on
$\mathbb {A}$
in random extensions of the set-theoretical universe. This appears to have strong connections with Dow and Fremlin’s result stating that there are Efimov spaces in the random model. We also investigate relations between topologies on
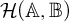 $\mathcal {H}(\mathbb {A},\mathbb {B})$
for a Boolean algebra
$\mathcal {H}(\mathbb {A},\mathbb {B})$
for a Boolean algebra
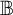 $\mathbb {B}$
carrying a strictly positive measure and convergence properties of sequences of measures on
$\mathbb {B}$
carrying a strictly positive measure and convergence properties of sequences of measures on
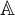 $\mathbb {A}$
.
$\mathbb {A}$
.
Keywords
MSC classification
- Type
- Article
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press on behalf of The Association for Symbolic Logic
References
- 2
- Cited by



