Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Hyttinen, Tapani
and
Tuuri, Heikki
1991.
Constructing strongly equivalent nonisomorphic models for unstable theories.
Annals of Pure and Applied Logic,
Vol. 52,
Issue. 3,
p.
203.
Hyttinen, Tapani
and
Hyttinen, T.
1992.
ON NON‐DETERMINED EHRENFEUCHT‐FRAÏSSÉ GAMES AND UNSTABLE THEORIES.
Mathematical Logic Quarterly,
Vol. 38,
Issue. 1,
p.
399.
Mekler, Alan
and
Oikkonen, Juha
1993.
Abelian p-groups with no invariants.
Journal of Pure and Applied Algebra,
Vol. 87,
Issue. 1,
p.
51.
Oikkonen, Juha
and
Väänänen, Jouko
1993.
Game-theoretic inductive definability.
Annals of Pure and Applied Logic,
Vol. 65,
Issue. 3,
p.
265.
Huuskonen, Taneli
1995.
Observations about Scott and Karp trees.
Annals of Pure and Applied Logic,
Vol. 76,
Issue. 3,
p.
201.
Väänänen, Jouko
1995.
Quantifiers: Logics, Models and Computation.
p.
105.
Eklof, Paul C.
and
Mekler, Alan H.
2002.
Almost Free Modules - Set-theoretic Methods.
Vol. 65,
Issue. ,
p.
123.
Eklof, Paul C.
2002.
Almost Free Modules - Set-theoretic Methods.
Vol. 65,
Issue. ,
p.
85.
Eklof, Paul C.
and
Mekler, Alan H.
2002.
Almost Free Modules - Set-theoretic Methods.
Vol. 65,
Issue. ,
p.
143.
Eklof, Paul C.
and
Mekler, Alan H.
2002.
Almost Free Modules - Set-theoretic Methods.
Vol. 65,
Issue. ,
p.
17.
Eklof, Paul C.
and
Mekler, Alan H.
2002.
Almost Free Modules - Set-theoretic Methods.
Vol. 65,
Issue. ,
p.
401.
Eklof, Paul C.
and
Mekler, Alan H.
2002.
Almost Free Modules - Set-theoretic Methods.
Vol. 65,
Issue. ,
p.
316.
Eklof, Paul C.
2002.
Almost Free Modules - Set-theoretic Methods.
Vol. 65,
Issue. ,
p.
363.
Eklof, Paul C.
and
Mekler, Alan H.
2002.
Almost Free Modules - Set-theoretic Methods.
Vol. 65,
Issue. ,
p.
527.
Eklof, Paul C.
and
Mekler, Alan H.
2002.
Almost Free Modules - Set-theoretic Methods.
Vol. 65,
Issue. ,
p.
441.
Eklof, Paul C.
2002.
Almost Free Modules - Set-theoretic Methods.
Vol. 65,
Issue. ,
p.
328.
Eklof, Paul C.
and
Mekler, Alan H.
2002.
Almost Free Modules - Set-theoretic Methods.
Vol. 65,
Issue. ,
p.
292.
Eklof, Paul C.
and
Mekler, Alan H.
2002.
Almost Free Modules - Set-theoretic Methods.
Vol. 65,
Issue. ,
p.
476.
Eklof, Paul C.
and
Mekler, Alan H.
2002.
Almost Free Modules - Set-theoretic Methods.
Vol. 65,
Issue. ,
p.
55.
Eklof, Paul C.
and
Mekler, Alan H.
2002.
Almost Free Modules - Set-theoretic Methods.
Vol. 65,
Issue. ,
p.
264.
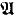 and
and 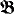 be two countable relational models of the same first order language. If the models are nonisomorphic, there is a unique countable ordinal α with the property that
be two countable relational models of the same first order language. If the models are nonisomorphic, there is a unique countable ordinal α with the property that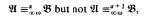
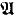 and
and 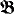 are L∞ω-equivalent up to quantifier-rank α but not up to α + 1. In this paper we consider models
are L∞ω-equivalent up to quantifier-rank α but not up to α + 1. In this paper we consider models 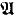 and
and 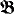 of cardinality ω1 and construct trees which have a similar relation to
of cardinality ω1 and construct trees which have a similar relation to 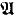 and
and 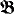 as a above. For this purpose we introduce a new ordering T ≪ T′ of trees, which may have some independent interest of its own. It turns out that the above ordinal α has two qualities which coincide in countable models but will differ in uncountable models. Respectively, two kinds of trees emerge from α. We call them Scott trees and Karp trees, respectively. The definition and existence of these trees is based on an examination of the Ehrenfeucht game of length ω1 between
as a above. For this purpose we introduce a new ordering T ≪ T′ of trees, which may have some independent interest of its own. It turns out that the above ordinal α has two qualities which coincide in countable models but will differ in uncountable models. Respectively, two kinds of trees emerge from α. We call them Scott trees and Karp trees, respectively. The definition and existence of these trees is based on an examination of the Ehrenfeucht game of length ω1 between 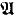 and
and 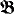 . We construct two models of power ω1 with
. We construct two models of power ω1 with 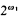 mutually noncomparable Scott trees.
mutually noncomparable Scott trees.

