ON REALS WITH 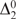${\rm{\Delta }}_2^0$-BOUNDED COMPLEXITY AND COMPRESSIVE POWER

Abstract

The (prefix-free) Kolmogorov complexity of a finite binary string is the length of the shortest description of the string. This gives rise to some ‘standard’ lowness notions for reals: A is K-trivial if its initial segments have the lowest possible complexity and A is low for K if using A as an oracle does not decrease the complexity of strings by more than a constant factor. We weaken these notions by requiring the defining inequalities to hold only up to all 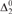${\rm{\Delta }}_2^0$ orders, and call the new notions 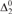${\rm{\Delta }}_2^0$-bounded K-trivial and 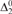${\rm{\Delta }}_2^0$-bounded low for K. Several of the ‘nice’ properties of K-triviality are lost with this weakening. For instance, the new weaker definitions both give uncountable set of reals. In this paper we show that the weaker definitions are no longer equivalent, and that the 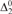${\rm{\Delta }}_2^0$-bounded K-trivials are cofinal in the Turing degrees. We then compare them to other previously studied weakenings, namely infinitely-often K-triviality and weak lowness for K (in each, the defining inequality must hold up to a constant, but only for infinitely many inputs). We show that 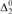${\rm{\Delta }}_2^0$-bounded K-trivial implies infinitely-often K-trivial, but no implication holds between 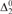${\rm{\Delta }}_2^0$-bounded low for K and weakly low for K.