Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Valizadeh, Ali N.
and
Pourmahdian, Massoud
2020.
Pseudofiniteness in Hrushovski Constructions.
Notre Dame Journal of Formal Logic,
Vol. 61,
Issue. 1,
Elwes, Richard
2021.
Evolving Shelah‐Spencer graphs.
Mathematical Logic Quarterly,
Vol. 67,
Issue. 1,
p.
6.
Kikyo, Hirotaka
and
Tsuboi, Akito
2024.
Random structures and automorphisms with a single orbit.
Archive for Mathematical Logic,


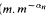 ). We show that in most cases the model theory is either extremely well-behaved or extremely wild, and characterize when each occurs.
). We show that in most cases the model theory is either extremely well-behaved or extremely wild, and characterize when each occurs.