Article contents
On projective ordinals1
Published online by Cambridge University Press: 12 March 2014
Extract
We study in this paper the projective ordinals 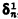 , where
, where 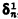 = sup{ξ: ξis the length of a Δn 1prewellordering of the continuum}. These ordinals were introduced by Moschovakis in [8] to serve as a measure of the “definable length” of the continuum. We prove first in §2 that projective determinacy implies
= sup{ξ: ξis the length of a Δn 1prewellordering of the continuum}. These ordinals were introduced by Moschovakis in [8] to serve as a measure of the “definable length” of the continuum. We prove first in §2 that projective determinacy implies 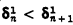 , for all even n > 0 (the same result for odd n is due to Moschovakis). Next, in the context of full determinacy, we partly generalize (in §3) the classical fact that δ1 1 = ℵ1 and the result of Martin that δ3 1 = ℵω+1 by proving that
, for all even n > 0 (the same result for odd n is due to Moschovakis). Next, in the context of full determinacy, we partly generalize (in §3) the classical fact that δ1 1 = ℵ1 and the result of Martin that δ3 1 = ℵω+1 by proving that 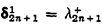 , where λ2n+1 is a cardinal of cofinality ω. Finally we discuss in §4 the connection between the projective ordinals and Solovay's uniform indiscernibles. We prove among other things that ∀α(α # exists) implies that every δn 1 with n ≥ 3 is a fixed point of the increasing enumeration of the uniform indiscernibles.
, where λ2n+1 is a cardinal of cofinality ω. Finally we discuss in §4 the connection between the projective ordinals and Solovay's uniform indiscernibles. We prove among other things that ∀α(α # exists) implies that every δn 1 with n ≥ 3 is a fixed point of the increasing enumeration of the uniform indiscernibles.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1974
Footnotes
The results in this paper are included in the author's doctoral dissertation submitted to the University of California, Los Angeles, in June 1972. The author would like to express his sincerest thanks to his thesis advisor, Professor Yiannis N. Moschovakis, both for creating his interest in descriptive set theory and for his guidance and encouragement. The preparation of the paper was partially supported by NSF grant GP-27964.
References
REFERENCES
- 15
- Cited by


