Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Brooke-Taylor, A.
and
Rosický, J.
2016.
Accessible images revisited.
Proceedings of the American Mathematical Society,
Vol. 145,
Issue. 3,
p.
1317.
Hušek, M.
and
Rosický, J.
2019.
Factorization and local presentability in topological and uniform spaces.
Topology and its Applications,
Vol. 259,
Issue. ,
p.
251.
Usuba, Toshimichi
2019.
A note on the tightness of G-modifications.
Topology and its Applications,
Vol. 265,
Issue. ,
p.
106820.
Lieberman, Michael
Rosický, Jiří
and
Vasey, Sebastien
2019.
Internal sizes in μ-abstract elementary classes.
Journal of Pure and Applied Algebra,
Vol. 223,
Issue. 10,
p.
4560.
Dow, A.
Juhász, I.
Soukup, L.
Szentmiklóssy, Z.
and
Weiss, W.
2019.
On the tightness of
$${G_\delta}$$
G
δ
-modifications.
Acta Mathematica Hungarica,
Vol. 158,
Issue. 2,
p.
294.
Usuba, Toshimichi
2021.
A note on δ-strongly compact cardinals.
Topology and its Applications,
Vol. 301,
Issue. ,
p.
107538.
HAYUT, YAIR
MAGIDOR, MENACHEM
and
POVEDA, ALEJANDRO
2022.
IDENTITY CRISIS BETWEEN SUPERCOMPACTNESS AND VǑPENKA’S PRINCIPLE.
The Journal of Symbolic Logic,
Vol. 87,
Issue. 2,
p.
626.
Goldberg, Gabriel
2022.
Strong compactness and the ultrapower axiom I: the least strongly compact cardinal.
Journal of Mathematical Logic,
Vol. 22,
Issue. 02,
BAGARIA, JOAN
and
POVEDA, ALEJANDRO
2023.
MORE ON THE PRESERVATION OF LARGE CARDINALS UNDER CLASS FORCING.
The Journal of Symbolic Logic,
Vol. 88,
Issue. 1,
p.
290.
Bagaria, Joan
and
da Silva, Samuel G.
2023.
ω1-strongly compact cardinals and normality.
Topology and its Applications,
Vol. 323,
Issue. ,
p.
108276.
Hušek, M.
2023.
G-covers and ω1-strongly compact cardinals.
Topology and its Applications,
Vol. 338,
Issue. ,
p.
108652.
Hirata, Yasushi
and
Yajima, Yukinobu
2024.
Dual discreteness of Σ-products and irreducibility of infinite products.
Topology and its Applications,
Vol. 356,
Issue. ,
p.
109032.
YOU, ZHIXING
and
YUAN, JIACHEN
2024.
ON THE COFINALITY OF THE LEAST
$\lambda $
-STRONGLY COMPACT CARDINAL.
The Journal of Symbolic Logic,
Vol. 89,
Issue. 2,
p.
569.
Poveda, Alejandro
2024.
Two results on extendible cardinals.
Proceedings of the American Mathematical Society,
Bagaria, Joan
and
Lücke, Philipp
2024.
Patterns of structural reflection in the large-cardinal hierarchy.
Transactions of the American Mathematical Society,
Gitman, Victoria
and
Osinski, Jonathan
2025.
Upward Löwenheim-Skolem-Tarski numbers for abstract logics.
Annals of Pure and Applied Logic,
Vol. 176,
Issue. 8,
p.
103583.
You, Zhixing
and
Yuan, Jiachen
2025.
How far is almost strong compactness from strong compactness.
Journal of Mathematical Logic,
Vol. 25,
Issue. 01,
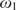 ${\omega _1}$-STRONGLY COMPACT CARDINALS
${\omega _1}$-STRONGLY COMPACT CARDINALS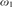 ${\omega _1}$-strongly compact if every
κ-complete ultrafilter on any set I
can be extended to an
${\omega _1}$-strongly compact if every
κ-complete ultrafilter on any set I
can be extended to an 
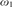 ${\omega _1}$-strongly compact cardinal,
${\omega _1}$-strongly compact cardinal, 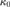 ${\kappa _0}$, cannot be a successor cardinal, and that its cofinality is at
least the first measurable cardinal. We prove that the Singular Cardinal
Hypothesis holds above
${\kappa _0}$, cannot be a successor cardinal, and that its cofinality is at
least the first measurable cardinal. We prove that the Singular Cardinal
Hypothesis holds above 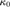 ${\kappa _0}$. We show that the product of Lindelöf spaces is
κ-Lindelöf if and only if
${\kappa _0}$. We show that the product of Lindelöf spaces is
κ-Lindelöf if and only if 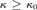 $\kappa \ge {\kappa _0}$. Finally, we characterize
$\kappa \ge {\kappa _0}$. Finally, we characterize 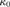 ${\kappa _0}$ in terms of second order reflection for relational structures
and we give some applications. For instance, we show that every first-countable
nonmetrizable space has a nonmetrizable subspace of size less than
${\kappa _0}$ in terms of second order reflection for relational structures
and we give some applications. For instance, we show that every first-countable
nonmetrizable space has a nonmetrizable subspace of size less than 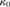 ${\kappa _0}$.
${\kappa _0}$.