Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-07T22:19:40.214Z Has data issue: false hasContentIssue false
  • English
  • Français

On ideals and stationary reflection

Published online by Cambridge University Press:  12 March 2014

C. A. Johnson
C. A. Johnson*
Affiliation:
Department of Mathematics, University of Keele, Keele, Staffordshire ST5 5BG, England
Get access Rights & Permissions [Opens in a new window]

Extract

It is a theorem of Prikry [7] that if κ carries a uniform η-descendingly complete ultrafilter then the stationary reflection property 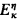fails. In this paper we will derive similar results, but here from properties of filters (or ideals) rather than ultrafilters.

Throughout κ and η will denote regular cardinals with η < κ (in particular κ will be uncountable), and I will denote an ideal on κ, by which we mean a set I ⊆ P(κ) such that (i) I is closed under taking subsets and finite unions and (ii) αЄ I for each α < κ, but κ ∉ I. I is said to be μ-complete if it is closed under taking unions of size < μ, I* = {X ⊆ κ ∣ κ − X Є I} is the filter dual to I and if A Є I+ (= P(κ) − I), then I∣A is the ideal on κ given by I ∣ A = {X ⊆ κ ∣ X ∩ A Є I}. If h: A → κ then h is said to be (i) unbounded mod I if for each α < κ, h−1(α) = {ξ Є A ∣ h(ξ) < α} Є I and (ii) a least function for I if h is unbounded mod I and whenever g: A → κ is a function, unbounded mod I, then {ξ Є A ∣ g{ξ) < h{ξ)} Є I.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 54 , Issue 2 , June 1989 , pp. 568 - 575
Copyright
Copyright © Association for Symbolic Logic 1989

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Carr, D. M., The structure of ineffability properties of Pκλ (preprint).Google Scholar
[2]Galvin, F., Jech, T., and Magidor, M., An ideal game, this Journal, vol. 43 (1978), pp. 284–291.Google Scholar
[3]Jech, T. and Prikry, K., Ideals over uncountable sets, Memoir no. 214, American Mathematical Society, Providence, Rhode Island, 1979.Google Scholar
[4]Kanamori, A., Weakly normal filters and irregular ultrafilters, Transactions of the American Mathematical Society, vol. 220 (1976), pp. 393–399.CrossRefGoogle Scholar
[5]Kanamori, A. and Magidor, M., The evolution of large cardinal axioms in set theory, Higher set theory (proceedings, Oberwolfach, 1977), Lecture Notes in Mathematics, vol. 699, Springer-Verlag, Berlin, 1978, pp. 99–275.CrossRefGoogle Scholar
[6]Komjath, P., Stationary reflection for uncountable cofinality, this Journal, vol. 51 (1986), pp. 147–151.Google Scholar
[7]Prikry, K., On descendingly complete ultrafilters, Cambridge summer school in mathematical logic (1971), Lecture Notes in Mathematics, vol. 337, Springer-Verlag, Berlin, 1973, pp. 459–488.CrossRefGoogle Scholar
[8]Solovay, R. M., Reinhardt, W. N., and Kanamori, A., Strong axioms of infinity and elementary embeddings, Annals of Mathematical Logic, vol. 13 (1978), pp. 73–116.CrossRefGoogle Scholar
[9]Takahashi, J., A saturation property of ideals and weakly compact cardinals, this Journal, vol. 51 (1986), pp. 513–525.Google Scholar