Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-29T11:03:10.730Z Has data issue: false hasContentIssue false
  • English
  • Français

On generalized quantifiers in arithmetic

Published online by Cambridge University Press:  12 March 2014

Carl Morgenstern
Carl Morgenstern*
Affiliation:
University of Colorado, Colorado Springs, Colorado 80907
Get access Rights & Permissions [Opens in a new window]

Extract

In this note we investigate an extension of Peano arithmetic which arises from adjoining generalized quantifiers to first-order logic. Markwald [2] first studied the definability properties of L1, the language of first-order arithmetic, L, with the additional quantifer Ux which denotes “there are infinitely many x such that…. Note that Ux is the same thing as the Keisler quantifier Qx in the ℵ0 interpretation.

We consider L2, which is L together with the ℵ0 interpretation of the Magidor-Malitz quantifier Q2xy which denotes “there is an infinite set X such that for distinct x, y ∈ X …”. In [1] Magidor and Malitz presented an axiom system for languages which arise from adding Q2 to a first-order language. They proved that the axioms are valid in every regular interpretation, and, assuming ◊ω1, that the axioms are complete in the ℵ1 interpretation.

If we let 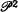denote Peano arithmetic in L2 with induction for L2 formulas and the Magidor-Malitz axioms as logical axioms, we show that in 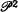we can give a truth definition for first-order Peano arithmetic, 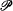. Consequently we can prove in 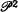that 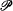is Πn sound for every n, thus in 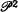we can prove the Paris-Harrington combinatorial principle and the higher-order analogues due to Schlipf.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 47 , Issue 1 , March 1982 , pp. 187 - 190
Copyright
Copyright © Association for Symbolic Logic 1982

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Magidor, M. and Malitz, J., Compact extensions of L(Q). Part la, Annals of Mathematical Logic, vol. 11 (1977), pp. 217–261.CrossRefGoogle Scholar
[2]Markwald, M., Zur Theorie der konstruktiven Wohlordmmgen, Mathematische Annalen, vol. 127 (1954), pp. 135–149.CrossRefGoogle Scholar
[3]Schoenfield, J., Mathematical logic, Addison-Wesley, Reading, Massachusetts, 1967.Google Scholar
[4]Takeuti, G., Proof theory, North-Holland, Amsterdam, 1975.Google Scholar