On decomposition of Gödelnumberings into Friedbergnumberings

Extract

The category of enumerations over P₁ is investigated. Objects are the enumerations of the set of partial recursive functions in one variable φ: N → P₁ where φ is a total effective function from the natural numbers N onto P₁.

To each a ∈ P₁ we call φ⁻¹(a) the set of all indices for a, the fibre over a.

Morphisms from one enumeration φ to another one ψ are (partial) recursive functions f, for which φ(n) = ψ(f(n)) holds for all n where f is denned, i.e. f is fibrepreserving. They are also called translators if f is total. The existence of a translator induces a partial ordering on the enumerations:

Let φ ≤ ψ, iff there exists a translator f with φ = ψ·f; φ ≡ ψ iff φ ≤ ψ and ψ ≤ φ. Two enumerations are called incomparable iff φ ≰,ψ and ψ ≰ φ.

Given a recursively enumerable family of enumerations {φⁱ}_i∈ω then their direct sum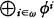 = π is defined by a bijective recursive pairing function g(i, n) (e.g. g(i, n) = (i + n)(i + n + 1)/2 + i) summing up the φⁱ by φⁱ(n) = 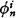= π_{g(i, n)} into π. We also say π decomposes into .

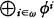Direct sums satisfy the universal property of sums in categories.

We want to operate decompositiontheory on special kinds of objects in our category, the Gödelnumberings and the Friedbergnumberings.

A Gödelnumbering φ is defined by (a) enumeration theorem (i.e. φ is object of our category) and (b) 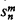-theorem, which means that each m + n-place p.r. function can be effectively replaced by an enumeration of n-place p.r. functions given by means of the total 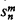-function (see Rogers [3]).