No CrossRef data available.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Published online by Cambridge University Press: 01 May 2018
We continue our study of the class 
${\cal C}\left( D \right)$, where D is a uniform ultrafilter on a cardinal κ and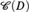 
${\cal C}\left( D \right)$ is the class of all pairs 
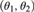$\left( {{\theta _1},{\theta _2}} \right)$, where 
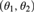$\left( {{\theta _1},{\theta _2}} \right)$ is the cofinality of a cut in 
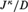${J^\kappa }/D$ and J is some 
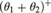${\left( {{\theta _1} + {\theta _2}} \right)^ + }$-saturated dense linear order. We give a combinatorial characterization of the class 
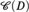${\cal C}\left( D \right)$. We also show that if 
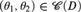$\left( {{\theta _1},{\theta _2}} \right) \in {\cal C}\left( D \right)$ and D is 
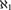${\aleph _1}$-complete or 
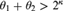${\theta _1} + {\theta _2} > {2^\kappa }$, then 
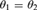${\theta _1} = {\theta _2}$.