No CrossRef data available.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Published online by Cambridge University Press: 12 March 2014
The following fairly elementary result seems to raise possibilities for the study of countable models of a theory in a countable language. For the terminology of model theory we refer to [CK].
Let L be a countable first-order language. Let L′ be the relational language having, for each formula φ of L and each sequence υ1,…,υn of variables including the free variables of φ, an n-ary relation symbol Pφ. For any L-structure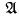 
and any formula Ψ(υ) of L, we define the Ψ-fraction of 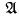to be the L′-structure 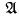Ψ whose universe consists of those elements of 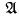satisfying Ψ(υ) and whose relations {Rφ}φϵL are defined by letting a1,…,an satisfy Rφ in 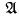Ψ if, and only if, a1,…, an satisfy φ in .
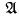An L-elementary class means the class of all L-structures satisfying each of some set of sentences of L. The countable part of an L-elementary class K means the class of all countable L-structures from K.
Theorem. Let K be an L-elementary class and let Ψ(υ) be a formula of L. Then the class of countable Ψ-fractions of structures in K is the countable part of some L′-elementary class.
Comment. By the downward Löwenheim-Skolem theorem, the countable Ψ-fractions of structures in K are the same as the Ψ-fractions of countable structures in K.
Proof. We give a set Σ′ of L′-sentences whose countable models are exactly the countable Ψ-fractions of structures in K.