Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-28T21:33:37.520Z Has data issue: false hasContentIssue false
  • English
  • Français

ON CONSTRAINTS AND DIVIDING IN TERNARY HOMOGENEOUS STRUCTURES

Published online by Cambridge University Press:  21 December 2018

VERA KOPONEN
VERA KOPONEN*
Affiliation:
DEPARTMENT OF MATHEMATICS UPPSALA UNIVERSITY, BOX 480, 75106UPPSALA, SWEDENE-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 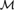${\cal M}$ be ternary, homogeneous and simple. We prove that if 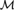${\cal M}$ is finitely constrained, then it is supersimple with finite SU-rank and dependence is k-trivial for some k < ω and for finite sets of real elements. Now suppose that, in addition, 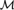${\cal M}$ is supersimple with SU-rank 1. If 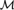${\cal M}$ is finitely constrained then algebraic closure in 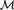${\cal M}$ is trivial. We also find connections between the nature of the constraints of 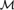${\cal M}$, the nature of the amalgamations allowed by the age of 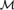${\cal M}$, and the nature of definable equivalence relations. A key method of proof is to “extract” constraints (of 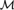${\cal M}$) from instances of dividing and from definable equivalence relations. Finally, we give new examples, including an uncountable family, of ternary homogeneous supersimple structures of SU-rank 1.

Keywords

Primary 03C10Secondary 03C4503C1303C1503C30model theoryhomogeneous structuresimple theoryconstraintdividingamalgamation
Type
Articles
Information
The Journal of Symbolic Logic , Volume 83 , Issue 4 , December 2018 , pp. 1691 - 1721
Copyright
Copyright © The Association for Symbolic Logic 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Ahlman, O., Simple theories axiomatized by almost sure theories. Annals of Pure and Applied Logic, vol. 167 (2016), pp. 435–456.CrossRefGoogle Scholar
Ahlman, O. and Koponen, V., On sets with rank one in simple homogeneous structures. Fundamenta Mathematicae, vol. 228 (2015), pp. 223–250.CrossRefGoogle Scholar
Akhtar, R. and Lachlan, A. H., On countable homogeneous 3-hypergraphs. Archive for Mathematical Logic, vol. 34 (1995), pp. 331–344.CrossRefGoogle Scholar
Bodirsky, M. and Pinsker, M., Reducts of Ramsey structures, Model Theoretic Methods in Finite Combinatorics (Grohe, M. and Makowsky, J. A., editors), Contemporary Mathematics, vol. 558, American Mathematical Society, Providence, RI, 2011, pp. 489–519.CrossRefGoogle Scholar
Casanovas, E., Simple Theories and Hyperimaginaries, Cambridge University Press, Cambridge, 2011.CrossRefGoogle Scholar
Cherlin, G. L., The Classification of Countable Homogeneous Directed Graphs and Countable Homogeneous n-tournaments, Memoirs of the American Mathematical Society, vol. 621, American Mathematical Society, Providence, RI, 1998.Google Scholar
Cherlin, G. and Hrushovski, E., Finite Structures with Few Types, Annals of Mathematics Studies, vol. 152, Princeton University Press, Princeton, NJ, 2003.Google Scholar
Conant, G., An axiomatic approach to free amalgamation, this JOURNAL, vol. 82 (2017), pp. 648–671.Google Scholar
Goode, J. B., Some trivial considerations, this JOURNAL, vol. 56 (1991), pp. 624–631.Google Scholar
Hell, P. and Nešetřil, J., Colouring, constraint satisfaction, and complexity. Computer Science Review, vol. 2 (2008), pp. 143–163.CrossRefGoogle Scholar
Henson, C. W., Countable homogeneous relational structures and ${\aleph _0}$-categorical theories, this JOURNAL, vol. 37 (1972), pp. 494–500.Google Scholar
Hodges, W., Model theory, Cambridge University Press, Cambridge, 1993.CrossRefGoogle Scholar
Hrushovski, E., Simplicity and the Lascar group, unpublished manuscript, 2003.Google Scholar
Kim, B., Simplicity Theory, Oxford University Press, Oxford, 2014.Google Scholar
Koponen, V., Binary simple homogeneous structures are supersimple with finite rank. Proceedings of the American Mathematical Society, vol. 144 (2016), pp. 1745–1759.CrossRefGoogle Scholar
Koponen, V., Binary primitive homogeneous simple structures, this JOURNAL, vol. 82 (2017), pp. 183–207.Google Scholar
Koponen, V., Binary simple homogeneous structures. Annals of Pure and Applied Logic, to appear, 2016, arXiv:1609.02433v1 [math.LO].Google Scholar
Koponen, V., Supersimple ω-categorical theories and pregeometries. Annals of Pure and Applied Logic, to appear, 2018, arXiv:1801.05748v2 [math.LO].Google Scholar
Kruckman, A., Infinitary limits of finite structures, Ph. D. thesis, University of California, Berkeley, 2016. Available at http://pages.iu.edu/∼akruckma/thesis.pdf.Google Scholar
Lachlan, A. H., Homogeneous structures, Proceedings of the International Congress of Mathematicians (Gleason, A. M., editor), American Mathematical Society, Providence, RI, 1986, pp. 314–321.Google Scholar
Lachlan, A. H., Stable finitely homogeneous structures: A survey, Algebraic Model Theory (Hart, B. T. et al. , editors), Kluwer Academic Publishers, Dordrecht, 1997, pp. 145–159.CrossRefGoogle Scholar
Lachlan, A. H. and Woodrow, R., Countable ultrahomogenous undirected graphs. Transactions of the Americal Mathematical Society, vol. 262 (1980), pp. 51–94.CrossRefGoogle Scholar
Macpherson, D., A survey of homogeneous structures. Discrete Mathematics, vol. 311 (2011), pp. 1599–1634.CrossRefGoogle Scholar
Nešetřil, J., Ramsey classes and homogeneous structures. Combinatorics, Probability and Computing, vol. 14 (2005), pp. 171–189.CrossRefGoogle Scholar
Palacín, D., Generalized amalgamation and homogeneity, this JOURNAL, vol. 82 (2017), pp. 1402–1421.Google Scholar
Schmerl, J. H., Countable homogeneous partially ordered sets. Algebra Universalis, vol. 9 (1979), pp. 317–321.CrossRefGoogle Scholar