Article contents
On closure under direct product
Published online by Cambridge University Press: 12 March 2014
Extract
In 1951, Horn obtained a sufficient condition for an arithmetical class to be closed under direct product. A natural question which arose was whether Horn's condition is also necessary. We obtain a negative answer to that question.
We shall discuss relational systems of the form
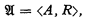
where A and R are non-empty sets; each element of R is an ordered triple 〈a, b, c〉, with a, b, c ∈ A.1 If the triple 〈a, b, c〉 belongs to the relation R, we write R(a, b, c); if 〈a, b, c〉 ∉ R, we write 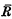 (a, b, c). If x0, x1 and x2 are variables, then R(x0, x1, x2) and x0 = x1 are predicates. The expressions
(a, b, c). If x0, x1 and x2 are variables, then R(x0, x1, x2) and x0 = x1 are predicates. The expressions 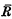 (x0, x1, x2) and x0 ≠ x1 will be referred to as negations of predicates.
(x0, x1, x2) and x0 ≠ x1 will be referred to as negations of predicates.
We speak of α1, …, αn as terms of the disjunction α1 ∨ … ∨ αn and as factors of the conjunction α1 ∧ … ∧ αn. A sentence (open, closed or neither) of the form
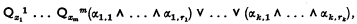
where each Qi (if there be any) is either the universal or the existential quantifier and each αi, l is either a predicate or a negation of a predicate, is said to be in prenex disjunctive normal form.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1958
References
BIBLIOGRAPHY
- 17
- Cited by


