Article contents
On carnap and popper probability functions
Published online by Cambridge University Press: 12 March 2014
Extract
With PC understood to be the propositional calculus of [3], call a binary function Pr from the wffs of PC to the reals a Carnap (probability) function if it meets requirements A1—A5 in Table I (with ‘⊢…’ short in A3—A4 for ‘… is a tautology’), and call the function a Popper (probability) function if it meets requirements Bl—B6 there:
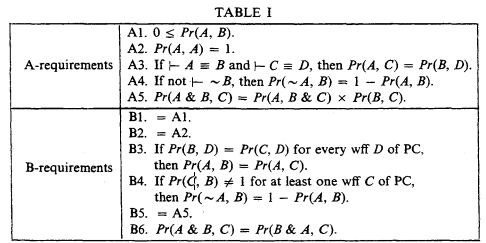
Leblanc established in [3] that every Carnap function is a Popper one, and he tendered proof of the converse. As reported by Stalnaker in [5], the proof unfortunately was incomplete, a mishap due to Leblanc's abbreviating ‘Pr(A, ∼ A) = 1’ as ‘⊢ A’ when Pr is a Popper function. Borrowing from [4], Leblanc did show, as Harper notes in [2, footnote 17], that
(1) If Pr is a Popper function and A is a tautology, then Pr(A, ∼ A) = 1. He did not, however, show that
(2) If Pr is a Popper function and Pr(A, ∼ A) = 1, then A is a tautology.
Nor could he have done so: (2) is false, as the simplest of counterexamples shows. Denied (2), Leblanc had no hope of proving that every Popper function is a Carnap one: of a Popper function Pr it is easily ascertained that Pr meets requirement A4 if and only if Pr(A, ∼ A) = 1 just in case A is a tautology.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1979
References
REFERENCES
- 10
- Cited by


