Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-27T01:37:25.468Z Has data issue: false hasContentIssue false
  • English
  • Français

On boolean subalgebras of 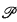(ω1)/ctble

Published online by Cambridge University Press:  12 March 2014

Alan Dow
Alan Dow*
Affiliation:
Department of Mathematics, York University, North York, Ontario, M3J 1P3, Canada, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

It is well known that every Boolean algebra of size ω1 can be embedded into 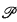(ω)/fin. E. van Douwen proved that if CH failed then there is a Boolean algebra of size ω2 which cannot be embedded into 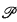(ω1)/ctble. We show that ◇ is equivalent to the statement that a certain natural Boolean algebra of size 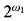embeds into 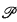(ω1)/ctble. I would like to thank B. Velickovic for many helpful conversations.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 61 , Issue 3 , September 1996 , pp. 873 - 879
Copyright
Copyright © Association for Symbolic Logic 1996

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Shelah, S., On cardinal invariants of the continuum, Axiomatic set theory, Contemporary Mathematics, American Mathematical Society, 1984.Google Scholar
[2]van Douwen, E. K., On question Q47, Topology and its Applications, vol. 39 (1991), pp. 33–42.CrossRefGoogle Scholar