Article contents
On analytic well-orderings
Published online by Cambridge University Press: 12 March 2014
Extract
Since about 1955, recursive, (hyper-)arithmetic and  well-orderings have been investigated by many authors. Now we shall generally consider analytic well-orderings and compare their representation-capacities for ordinals.
well-orderings have been investigated by many authors. Now we shall generally consider analytic well-orderings and compare their representation-capacities for ordinals.
Let K be a class of predicates. Then, R is called a Kwell-ordering if R is a binary relation of natural numbers belonging to the class K and satisfies the following conditions:
(i) R(x, y) ∧ R(y, x) → x = y;
(ii) x, y ∈ D(R) → R(x, y) ∨ R(y, x), where D(R) is the domain of R, that is to say, the set {x ∣ (∃y)[R(x, y) ∨ R(y, x)]};
(iii) R(x, y) ∧ R(y, z) → R(x, z);
(iv) 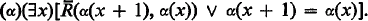 .
.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1970
References
- 6
- Cited by


