Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-08T01:23:11.994Z Has data issue: false hasContentIssue false
  • English
  • Français

On a set theory of bernays

Published online by Cambridge University Press:  12 March 2014

Leslie H. Tharp
Leslie H. Tharp*
Affiliation:
Massachusetts Institute of Technology
Get access Rights & Permissions [Opens in a new window]

Extract

We are concerned here with the set theory given in [1], which we call BL (Bernays-Levy). This theory can be given an elegant syntactical presentation which allows most of the usual axioms to be deduced from the reflection principle. However, it is more convenient here to take the usual Von Neumann-Bernays set theory [3] as a starting point, and to regard BL as arising from the addition of the schema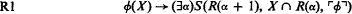

where S is the formal definition of satisfaction (with respect to models which are sets) and ┌φ┐ is the Gödel number of φ which has a single free variable X.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 32 , Issue 3 , 09 October 1967 , pp. 319 - 321
Copyright
Copyright © Association for Symbolic Logic 1967

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Bernays, P., Zur Frage der Unendlichkeitsschemata in der Axiomatischen Mengenlehre, Essays on the foundations of mathematics, Jerusalem, 1961, pp. 3–49.Google Scholar
[2]Davis, M., The undecidable, Raven Press, Hewlet, New York, 1965.Google Scholar
[3]Gödel, K., The consistency of the continuum hypothesis, Annals of Mathematics Studies, no. 3, Princeton Univ. Press, Princeton, N.J., 1940.CrossRefGoogle Scholar
[4]Hanf, W. P. and Scott, D., Classifying inaccessible cardinals, Notices of the American Mathematical Society, vol. 8 (1961), p. 445.Google Scholar
[5]Mostowski, A., Some impredicative definitions in the axiomatic set theory, Fundamenta mathematicae, vol. 37 (1950), p. 111.CrossRefGoogle Scholar
[6]Putnam, H. and Tharp, L., A general treatment of constructibility (to appear).Google Scholar
[7]Scott, D., Measurable cardinals and constructible sets, Bulletin de L'Académie Polonaise des Sciences (1959), pp. 521–524.Google Scholar
[8]Tharp, L., Bernays' set theory and the continuum hypothesis. Notices of the American Mathematical Society, vol. 13 (1966), p. 138.Google Scholar
[9]Tharp, L., Measurable cardinals amd Bernays' set theory, Notices of the American Mathematical Society, vol. 13 (1966), p. 233.Google Scholar