Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-18T15:13:48.833Z Has data issue: false hasContentIssue false
  • English
  • Français

ON A QUESTION OF KRAJEWSKI’S

Published online by Cambridge University Press:  14 March 2019

FEDOR PAKHOMOV  and
ALBERT VISSER
FEDOR PAKHOMOV
Affiliation:
DEPARTMENT OF MATHEMATICAL LOGIC STEKLOV MATHEMATICAL INSTITUTE 8 GUBKINA STREET, MOSCOW 119991RUSSIAE-mail: [email protected]
ALBERT VISSER
Affiliation:
PHILOSOPHY, FACULTY OF HUMANITIES UTRECHT UNIVERSITY, JANSKERKHOF 13 3512BL UTRECHT, THE NETHERLANDSE-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we study finitely axiomatizable conservative extensions of a theory U in the case where U is recursively enumerable and not finitely axiomatizable. Stanisław Krajewski posed the question whether there are minimal conservative extensions of this sort. We answer this question negatively.

Consider a finite expansion of the signature of U that contains at least one predicate symbol of arity ≥ 2. We show that, for any finite extension α of U in the expanded language that is conservative over U, there is a conservative extension β of U in the expanded language, such that 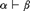$\alpha \vdash \beta$ and 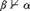$\beta \not \vdash \alpha$. The result is preserved when we consider either extensions or model-conservative extensions of U instead of conservative extensions. Moreover, the result is preserved when we replace $\dashv$ as ordering on the finitely axiomatized extensions in the expanded language by a relevant kind of interpretability, to wit interpretability that identically translates the symbols of the U-language.

We show that the result fails when we consider an expansion with only unary predicate symbols for conservative extensions of U ordered by interpretability that preserves the symbols of U.

Keywords

03B1003B3003F25predicate logicrecursively enumerable theoriesinterpretabilitylinear orderings
Type
Articles
Information
The Journal of Symbolic Logic , Volume 84 , Issue 1 , March 2019 , pp. 343 - 358
Copyright
Copyright © The Association for Symbolic Logic 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Barwise, J., Admissible Sets and Structures, Perspectives in Mathematical Logic, vol. 7, Cambridge University Press, Cambridge, 2017.Google Scholar
Buss, S. R., Bounded Arithmetic, Bibliopolis, Napoli, 1986.Google Scholar
Craig, W. and Vaught, R. L., Finite axiomatizability using additional predicates, this Journal, vol. 23 (1958), no. 3, pp. 289–308.Google Scholar
Friedman, H., Interpretations according to Tarski. This is one of the 2007 Tarski Lectures at Berkeley, 2007. The lecture is available at http://www.math.osu.edu/∼friedman.8/pdf/Tarski1,052407.pdf.Google Scholar
Fujimoto, K., Relative truth definability of axiomatic truth theories. Bulletin of Symbolic Logic, vol. 16 (2010), no. 3, pp. 305–344.10.2178/bsl/1286284556CrossRefGoogle Scholar
Hájek, P. and Pudlák, P., Metamathematics of First-Order Arithmetic, Perspectives in Mathematical Logic, Springer, Berlin, 1993.10.1007/978-3-662-22156-3CrossRefGoogle Scholar
Immerman, N., Descriptive Complexity, Springer Science & Business Media, New York, 2012.Google Scholar
Kleene, S. C., Finite axiomatizability of theories in the predicate calculus using additional predicate symbols, Two Papers on the Predicate Calculus, Memoirs of the American Mathematical Society, vol. 10, American Mathematical Society, Providence, RI, 1952, pp. 27–68.Google Scholar
Mycielski, J., Pudlák, P., and Stern, A. S., A Lattice of Chapters of Mathematics (Interpretations Between Theorems) , Memoirs of the American Mathematical Society, vol. 84, American Mathematical Society, Providence, RI, 1990.Google Scholar
Rubin, M., Theories of linear order. Israel Journal of Mathematics, vol. 17 (1974), no. 4, pp. 392–443.10.1007/BF02757141CrossRefGoogle Scholar
Tarski, A., A general theorem concerning the reduction of primitive notions, this Journal, vol. 19 (1954), pp. 158–159.Google Scholar
Tarski, A., Mostowski, A., and Robinson, R. M., Undecidable Theories, North–Holland, Amsterdam, 1953.Google Scholar
Visser, A., What is sequentiality? New Studies in Weak Arithmetics (Cégielski, P., Cornaros, C., and Dimitracopoulos, C., editors), CSLI Lecture Notes, vol. 211, CSLI Publications and Presses Universitaires du Pôle de Recherche et d’Enseingement Supérieur Paris-est, Stanford, 2013, pp. 229–269.Google Scholar
Visser, A., The interpretation existence lemma, Feferman on Foundations (Jäger, G. and Sieg, W., editors), Outstanding Contributions to Logic, vol. 13, Springer, Cham, 2017, pp. 101–144.10.1007/978-3-319-63334-3_5CrossRefGoogle Scholar
Visser, A., On Q. Soft Computing, vol. 21 (2017), no. 1, pp. 39–56.10.1007/s00500-016-2341-5CrossRefGoogle Scholar