Article contents
On a question of G. E. Sacks1
Published online by Cambridge University Press: 12 March 2014
Extract
In [1], p. 171, Sacks asks (question (Q5)) whether there is a recursively enumerable degree of unsolvability d such that
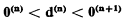 for all n ≧ 0. Sacks points out that the set of conditions which d must satisfy is not arithmetical. For this reason he suggests that a proof of (Q5) might require some new combinatorial device. The purpose of this note is to show how (Q5) may be proved simply by extending the methods of [l].2
for all n ≧ 0. Sacks points out that the set of conditions which d must satisfy is not arithmetical. For this reason he suggests that a proof of (Q5) might require some new combinatorial device. The purpose of this note is to show how (Q5) may be proved simply by extending the methods of [l].2
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1996
Footnotes
This paper was written while the author was a National Science Foundation Cooperative Fellow.
References
- 7
- Cited by


