Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-25T06:08:37.092Z Has data issue: false hasContentIssue false
  • English
  • Français

On a combinatorial property of menas related to the partition property for measures on supercompact cardinals

Published online by Cambridge University Press:  12 March 2014

Kenneth Kunen  and
Donald H. Pelletier
Kenneth Kunen*
Affiliation:
University of Texas at Austin, Austin, Texas 77712
Donald H. Pelletier
Affiliation:
York University, Downsview, Ontario, CanadaM3J 1P3
*
University of Wisconsin, Madison, Wisconsin 53706
Get access Rights & Permissions [Opens in a new window]

Abstract

T.K. Menas [4, pp. 225–234] introduced a combinatorial property Χ(μ) of a measure μ on a supercompact cardinal κ and proved that measures with this property also have the partition property. We prove here that Menas' property is not equivalent to the partition property. We also show that if a is the least cardinal greater than κ such that Pκα bears a measure without the partition property, then α is inaccessible and 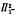-indescribable.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 48 , Issue 2 , June 1983 , pp. 475 - 481
Copyright
Copyright © Association for Symbolic Logic 1983

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Jech, T., Some combinatorial problems concerning uncountable cardinals, Annals of Mathematical Logic, vol. 5 (1973), pp. 165–198.CrossRefGoogle Scholar
[2]Kunen, K., Some remarks on theorems of Ketonen, Menas, and Solovay, unpublished hand-written manuscript, 1971, 4 pp.Google Scholar
[3]Magidor, M., Combinatorial characterization of supercompact cardinals, Proceedings of the American Mathematical Society, vol. 42 (1974), pp. 279–285.CrossRefGoogle Scholar
[4]Menas, T.K., A combinatorial property of pκλ, this Journal, vol. 41 (1976), pp. 225–234.Google Scholar
[5]Pelletier, D.H., A condition related to the partition property for measures on supercompact cardinals, Notices of the American Mathematical Society, vol. 26 (1979), p. A440.Google Scholar
[6]Pelletier, D.H., The partition property for certain extendible measures on supercompact cardinals, Proceedings of the American Mathematical Society, vol. 81 (1981), pp. 607–612.CrossRefGoogle Scholar
[7]Solovay, R., Reinhardt, W. and Kanamori, A., Strong axioms of infinity and elementary embeddings, Annals of Mathematical Logic, vol. 13 (1978), pp. 73–116.CrossRefGoogle Scholar