On a combinatorial principle of Hajnal and Komjáth

Extract

In their paper [3], Hajnal and Komjáth define the following combinatorial principle:

Definition 1.1. Suppose κ is an infinite cardinal and n < ω. Then H_n(κ) is the statement: There is a function F: [κ]ⁿ → [[κ]^ω]^≤ω such that

(a) ∀A ∈[κ]ⁿ ∀Y ∈ F(A)(Y ⊆ min (A)), and

(b) .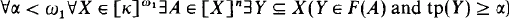

H_n(κ) is related to a more general principle introduced by Hajnal and Nagy in [4]. For applications of these principles to free sets for set mappings and Ramsey games we refer the reader to [3] and [4].

In [3] Hajnal and Komjáth prove the consistency of ZFC + GCH + ∀n ∈ ω(H_{n + 1}(ω_{n + 1})), relative to an ω-Mahlo cardinal. They conjecture that L is a model of this theory, and suggest that the proof might require higher gap morasses. The first few cases of this conjecture are known to be true; it is easy to see that if CH holds then H₁ (ω₁) is true, and Laver proved that V = L implies H₂(ω₂). In this paper we go one step further and prove V = L → H₃(ω₃). Unfortunately our methods do not appear to give H_n (ω_n) for n ≥ 4.

Most of our notation is standard. If X is any set and κ is a cardinal number then [X]^κ is the set of subsets of X with cardinality κ, and [X]^≤κ is the set of subsets of X with cardinality ≤ κ. If X is a set of ordinals then tp(X) is the order type of X.