Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T08:39:11.799Z Has data issue: false hasContentIssue false
  • English
  • Français

THE NUMBER OF ATOMIC MODELS OF UNCOUNTABLE THEORIES

Published online by Cambridge University Press:  08 February 2018

DOUGLAS ULRICH
DOUGLAS ULRICH*
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF MARYLAND COLLEGE PARK MD, USAE-mail:[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We show there exists a complete theory in a language of size continuum possessing a unique atomic model which is not constructible. We also show it is consistent with 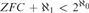$ZFC + {\aleph _1} < {2^{{\aleph _0}}}$ that there is a complete theory in a language of size 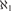${\aleph _1}$ possessing a unique atomic model which is not constructible. Finally we show it is consistent with 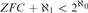$ZFC + {\aleph _1} < {2^{{\aleph _0}}}$ that for every complete theory T in a language of size 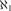${\aleph _1}$, if T has uncountable atomic models but no constructible models, then T has 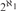${2^{{\aleph _1}}}$ atomic models of size 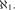${\aleph _1}$.

Keywords

03C55uncountable model theoryatomic modelsweak diamonduniformization
Type
Articles
Information
The Journal of Symbolic Logic , Volume 83 , Issue 1 , March 2018 , pp. 84 - 102
Copyright
Copyright © The Association for Symbolic Logic 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Baldwin, J., Categoricity, University Lecture Series, vol. 50, American Mathematical Society, Providence, RI, 2009.Google Scholar
Devlin, K. and Shelah, S., A weak version of $\diamondsuit$ which follows from ${2^{{\aleph _0}}} < {2^{{\aleph _1}}}$. Israel Journal of Mathematics, vol. 29 (1978), no. 2–3, pp. 239–247.Google Scholar
Knight, J., Prime and atomic models, this Journal, vol. 43 (1978), no. 3, pp. 385–393.Google Scholar
Kueker, D. W., Uniform theorems in infinitary logic, Logic Colloquium ’77 (Macintyre, A., Pacholski, L., and Paris, J., editors), North-Holland, Amsterdam, 1978, pp. 161–170.Google Scholar
Laskowski, M. C. and Shelah, S., On the existence of atomic models, this Journal, vol. 58 (1983), pp. 1189–1194.Google Scholar
Marcja, A. and Toffalori, C., A Guide to Classical and Modern Model Theory, Trends in Logic, vol. 19, Kluwer Academic Publishers, Dordrecht, The Netherlands, 2003.CrossRefGoogle Scholar
Newelski, L., Omitting types and the real line, this Journal, vol. 52 (1987), no. 4, pp. 1020–1026.Google Scholar
Rinot, A., Jensen’s diamond principle and its relatives, Set Theory and its Applications, Contemporary Mathematics, vol. 533, American Mathematical Society, Providence, RI, 2011, pp. 125–156.Google Scholar
Shelah, S., Categoricity in ${\aleph _1}$ of sentences in ${L_{{\omega _1}\omega }}\left( Q \right)$ Israel Journal of Mathematics, vol. 20 (1975), no. 2, pp. 127–148.CrossRefGoogle Scholar
Shelah, S., Classification Theory, North-Holland, Amsterdam, 1978.Google Scholar
Shelah, S., Classification theory for non-elementary classes I: The number of uncountable models of $\psi \in {L_{{\omega _1}\omega }}$. Israel Journal of Mathematics, vol. 46 (1983), no. 3, pp. 212–240.CrossRefGoogle Scholar
Shelah, S., Proper and Improper Forcing, second ed., Perspectives in Mathematical Logic, Springer-Verlag, Berlin, 1998.CrossRefGoogle Scholar
Shelah, S., On the uniqueness of prime models, this Journal, vol. 44 (1979), no. 2, pp. 215–220.Google Scholar
Shelah, S., Whitehead groups may not be free even assuming CH, II. Israel Journal of Mathematics, vol. 35 (1980), no. 4, pp. 257–285.CrossRefGoogle Scholar
Vaught, R., Denumerable models of complete theories. Infinitistic Methods (Proceedings of the Symposium on the Foundations of Mathematics, Warsaw 1959), Pergamon, 1961, pp. 303–321.Google Scholar