A note on interpretations of many-sorted theories

Extract

Whenever many-sorted theories are discussed in logic texts (e.g., [3, pp. 483–485]), it is fashionable to observe that every many-sorted theory 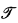can be effectively replaced by an equally powerful one-sorted theory 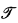*. The theory 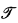* contains for each sort σ of 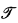a unary predicate symbol S_σ used to indicate that an individual is of sort σ; the nonlogical axioms of 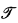* are the “translations” of those of 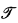together with axioms asserting that there is at least one individual of each sort and that all function symbols behave properly with respect to sorts. This observation suggests that perhaps many-sorted theories are no more useful than one-sorted theories. That this is not always the case has been pointed out previously [1, p. 13]. The content of this note is that 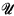can be interpretable in 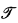without 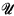* being interpretable in *.

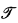If a function symbol f in a many-sorted theory takes as its arguments n terms a₁,…, a_n of sorts σ₁, …, σ_n, respectively and produces a term fa₁ … a_n of sort σ, then f is said to be of type (σ₁, …, σ_n;σ). Likewise, a predicate symbol is of type (σ₁, …, σ_n) if it takes as its arguments n terms of sorts σ₁, …, σ_n. We assume that for each sort σ there is a predicate symbol = _σ of type (σ, σ).