Article contents
A normalization theorem for set theory1
Published online by Cambridge University Press: 12 March 2014
Extract
In this paper we present a normalization theorem for a natural deduction formulation of Zermelo set theory. Our result gets around M. Crabbe's counterexample to normalizability (Hallnäs [3]) by adding an inference rule of the form

and requiring that this rule be used wherever it is applicable. Alternatively, we can regard the result as pertaining to a modified notion of normalization, in which an inference

is never considered reducible if A is T Є T, even if R is an elimination rule and the major premise of R is the conclusion of an introduction rule. A third alternative is to regard (1) as a derived rule: using the general well-foundedness rule
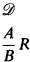
we can derive (1). If we regard (2) as neutral with respect to the normality of derivations (i.e., (2) counts as neither an introduction nor an elimination rule), then the resulting proofs are normal.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1988
Footnotes
This material is based upon work supported by the National Science Foundation under award number ISI-8560438. Any opinions, findings, and conclusions or recommendations expressed in this publication are those of the author and do not necessarily reflect the views of the National Science Foundation.
References
REFERENCES
- 3
- Cited by


